uncategorized

모두를 위한 딥러닝(1)

ML

모두를 위한 딥러닝 정리노트 #1

김성훈 교수님의 유투브강좌를 듣고 정리한 내용입니다.
https://www.youtube.com/watch?v=BS6O0zOGX4E&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm

Machine Learning

Limitation of explicit programming
  • spam filter : many rules
  • Automatic driving : too many rules

Machine Learning : 명시적으로 프로그래밍 하지 않아도 컴퓨터가 학습을 통해 어떠한 역할을 수행하는 것

Supervised / Unsupervised Learning

  • supervised Learning : 라벨링된 데이터로부터 학습하여 새로운 example에 대해 예측하는 것

    ex) 아파트 가격 예측, 시험 점수 예측 등..

  • unsupervised Learning : 라벨링이 안된 데이터로부터 그 데이터들을 그룹핑하는 것

    ex) Google new grouping : 연관된 이슈를 가진 뉴스끼리 자동으로 묶어줌

regression

: 연속적인 값을 가지는 output을 예측하는 것. - ex) 시험점수가 0 ~100 사이

Linear regression

아래표는 ‘학습시간’에 따른 기말고사 점수를 나타낸 표이다.

x(hours) y(score)
5 90
3 70
2 50
1 10

만약 몇 시간(x)동안 공부하면 몇 점(y)를 받을지 prediction(예측)하고 싶다고 하자.

학습시간과 점수는 정비례한다는 가설을 세우고 이문제에 대해 접근해보자.

가설함수
$$
H(x) = Wx +b
$$
를 위와 같이 정의하고 이를 그림으로 표현해보면

linear_reg_1

위와 같다. 파란점은 실제 데이터들이고, 빨간선은 우리가 세운 가설 H(x)이다. H(x)정도면 실제 데이터들의 값의 근사치를 예측할 수있겠다 싶은것이다.

그런데 그런 H(x)를 어떻게 찾을수 있을 것일까??

각 파란점들에서 빨간선으로 y축으로 내린 길이의 평균의 합이 가장 짧은 H(x)를 찾아보면 될거 같다. 그것이 모든 데이터들에 대해서 가장 근사하게 예측했다는 뜻이니까.

파란점에서 y축에 수직으로 내린 길이의 평균의 합을 어떻게 수식으로 표현할까?
$$
cost(W,b) = \frac{1}{m}\sum_{i=1}^m (H(x^i) - y^i)^2
$$
위와 같이 표현한다. H(x)가 W와 b에 관한 함수이기때문에 위와 같이 표현할 수 있다.

우리는 이것을 “cost” 함수라고 부를 것이고, cost 함수를 최소화 하는 것이 우리가 해야할 일이다.

Gradient Descent algorithm

cost 함수를 최소화 하기 위해서 우리는 gradient(경사) descent(하강) 알고리즘이라는 것을 사용할 것이다.

알고리즘을 사용하기 전에 그림을 그려 이해하기 편하도록 H(x)를 간소화 하자. 그러면 H(x)와 cost(W)는 다음과 같은 형태로 나타나게 된다.
$$
H(x) = Wx
$$

$$
cost(W) = \frac{1}{m}\sum_{i=1}^m (Wx^i - y^i)^2
$$

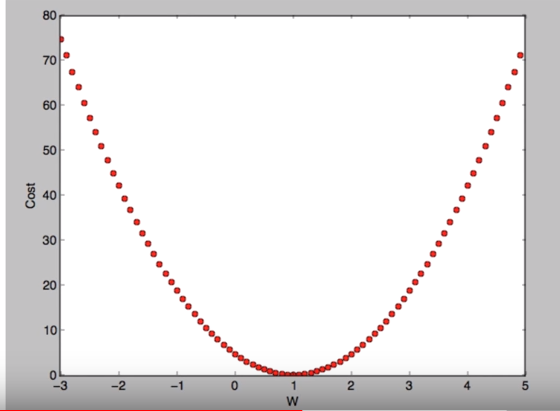
cost(W)가 어떻게 생겼는지 알기 위해 sample data를 가져와서 그려보자.

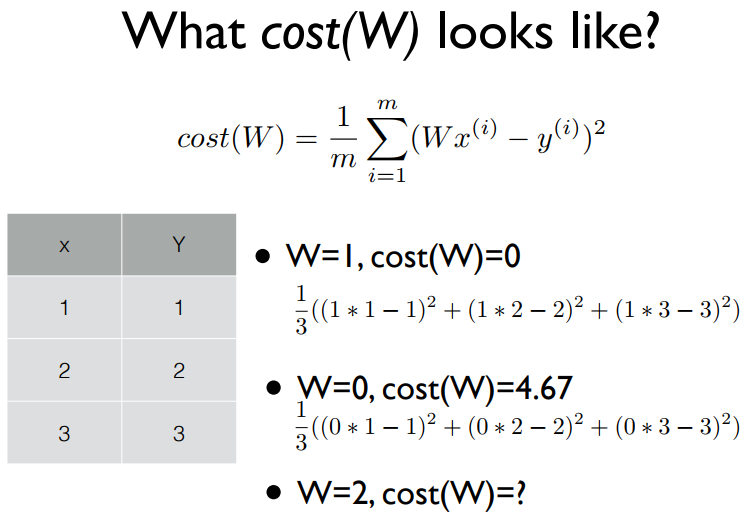
costW_look_like

W=2 일때는, cost(W) = 4.67 이다.

그러면 cost(W) 함수는 아래와 같이 그래프로 표현할 수 있는데,

gradient_descent_1

cost함수에서

  • 어느점에서 시작해도 상관없고,
  • W와 b를 약간씩 반복적으로 조정하면서 cost(W,b)를 최소화 하는 법을 찾는것

이 이 알고리즘의 핵심이다. - (여기서는 simplified hypothesis를 사용하므로 W만 조정)

반복적으로 어떻게 조정할것인가? 에서 경사타기가 시작된다. 경사타기는 아래 식과 같이 이루어진다.

$$
W:= W - \alpha\frac{\partial }{\partial W}cost(W)
$$
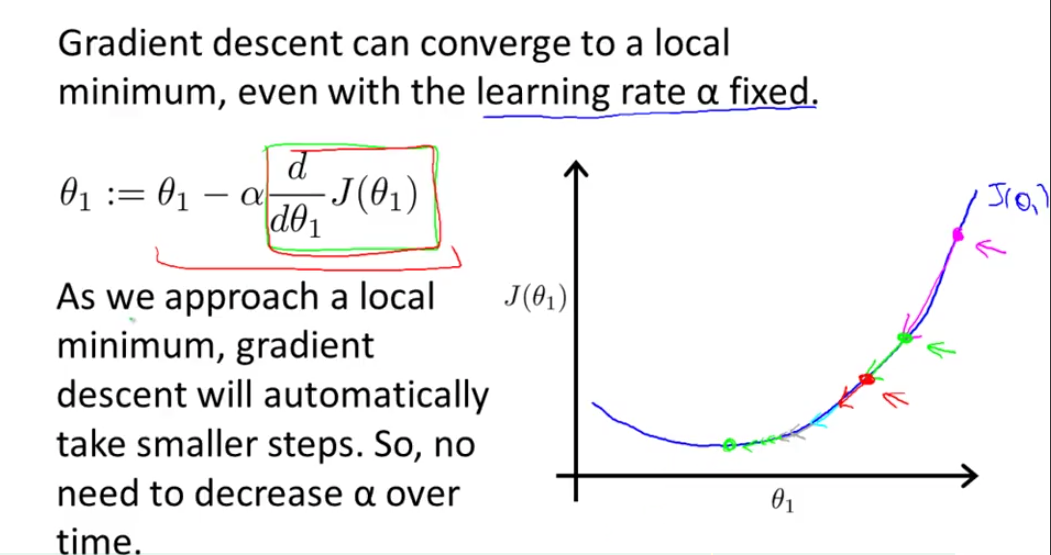
여기서 위의 a(알파)는 learning rate인데, 한번 경사를 탈때 얼마만큼 내려가나를 나타내는 상수이다.

coursera_ML_GD_autoSMALLSTEP

위 빨간색 박스의 미분값이 점차적으로 작아지므로 learning rate - alpha를 굳이 줄이지 않아도 자동적으로 작은 스텝으로 경사를 타고 내려 간다.

cost(W)함수는 이미 구한바 있으므로 위의 식에 대입해서 풀어보면

아래와 같은 식으로 표현할 수 있는데 1/m이 1/2m으로 변한건 미분한 결과값을 깔끔하게 보이기 위함이다.
$$
W:= W - \alpha\frac{\partial }{\partial W}\frac{1}{2m}\sum_{i=1}^m (H(x^i) - y^i)^2
$$

$$
W:= W - \alpha\frac{1}{2m}\sum_{i=1}^m 2(Wx^i - y^i)x^i
$$

$$
W:= W - \alpha\frac{1}{m}\sum_{i=1}^m (Wx^i - y^i)x^i
$$

미분을 하여 식을 정리해보면 맨 아래와 같은 Gradient descent 알고리즘의 식을 얻게된다.

위 알고리즘을 써서 cost(W)특정 점에서 경사를 타고 내려오면서, cost(W)를 최소화할 값을 찾는 것이다.

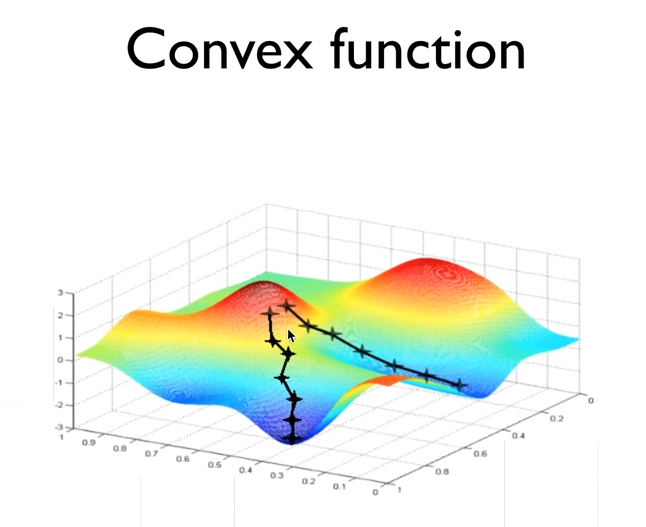
그럼 Gradient descent 알고리즘을 어디서나 쓸수있을까??

gradient_descent_convex_1

함수가 위와같으면 쓸수가없다. 어떤점에서 시작하는지에 따라 경사를 어디로 타는지 결정이 되고, 그에따라 “local minimum” 이 “global minimum”과 다른 현상이 나게 되므로,

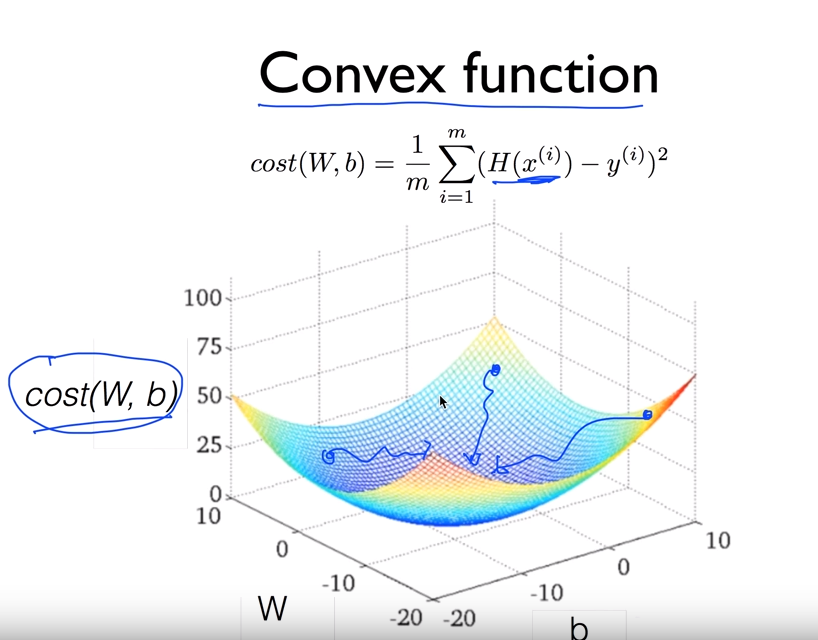
cost 함수의 모양이 다음과 같음을 확인하고 써야한다.

gradient_descent_convex_2

위와같은 함수를 convex function 이라고하고, 어떤 점에서 시작해도 global minimum에 도착한다.

Linear regression의 cost함수는 항상 convex function 형태로 나타난다.

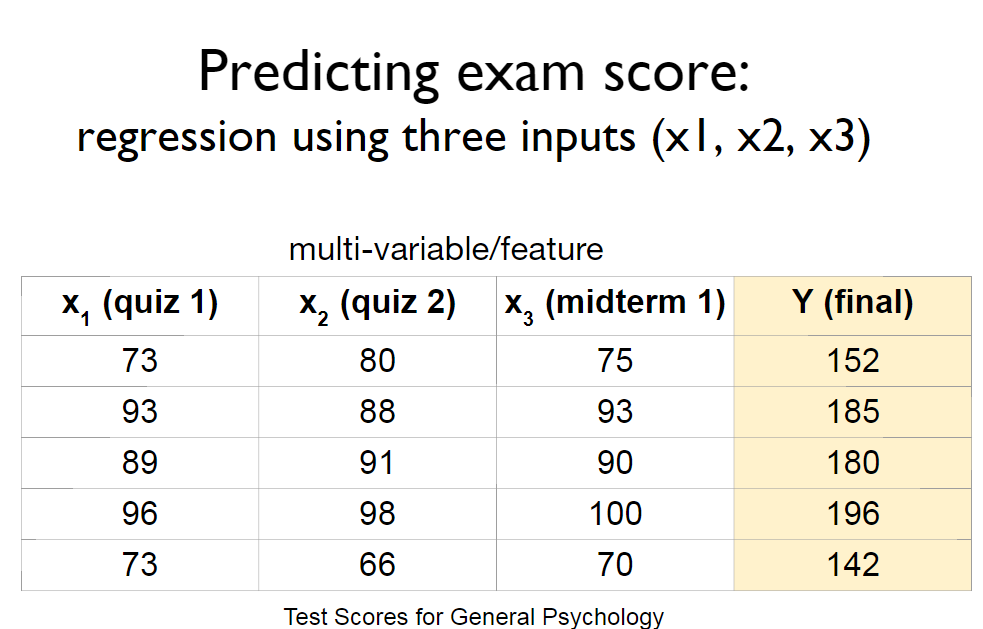
Multivariable linear regression

시험결과를 예측하는 우리의 문제에서 feature가 더 늘어났다고 하자.

multivariable_linear_regression_example

위와 같이 늘어난 feature가 n개로 늘어나게 되면 linear regression을 어떻게 적용할까?
$$
H(x) = Wx + b
$$

$$
H(x_1,x_2,x_3) = w_1x_1 + w_2x_2 + w_3x_3 + b
$$

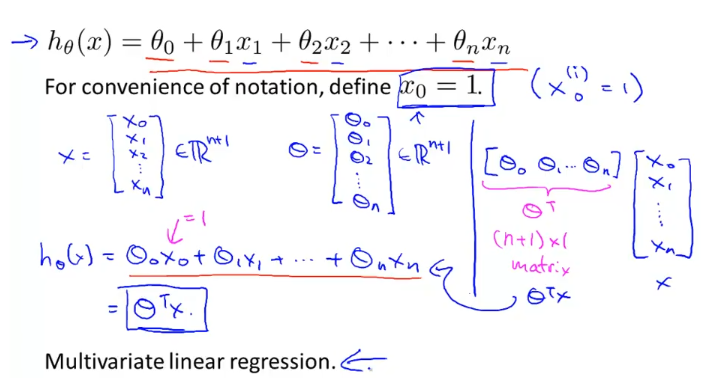
이것을 n개 로 일반화 하면 아래와 같이 표현되고
$$
H(x_1,x_2,x_3, …, x_n) = w_1x_1 + w_2x_2 + w_3x_3 + … + w_nx_n+b
$$
이것을 행렬의 곱 형태로 표현하면 아래와 같은 형태로 나타난다.

multivariable_hypothesis

(Binary) Classification

위까지는 선형 문제에 대한 가설을 세우고 그걸 풀어보는 것을 해보았다.

이제는 True / False로 주어지는 어떠한 문제

  • Spam or Ham
  • is cancer or not?

위와 같은 문제를 해결하기 위한 가설을 세우고 예측을 해볼 것이다.

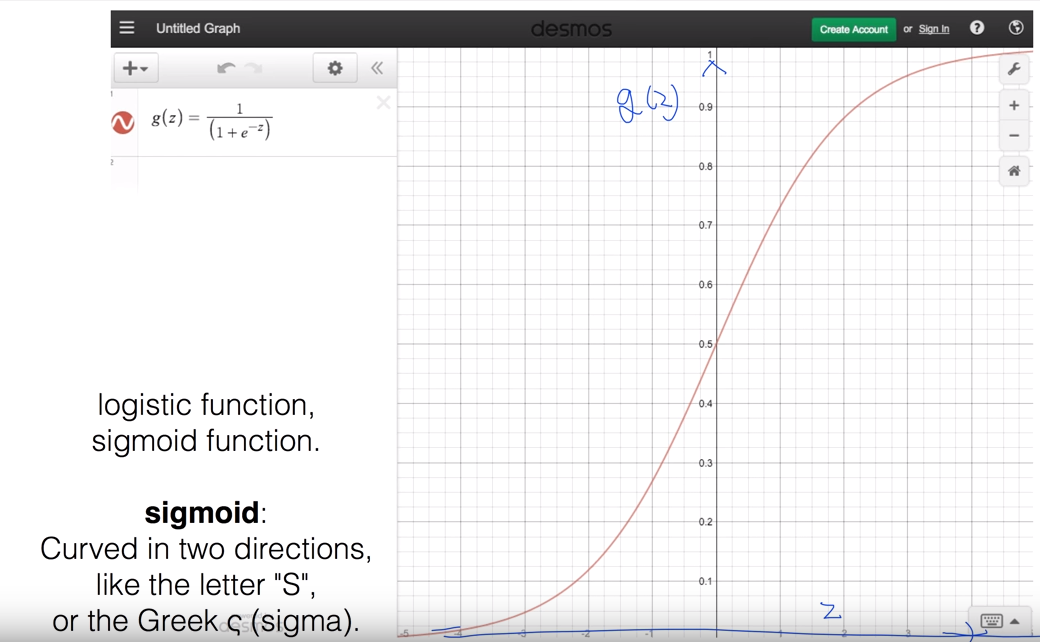
가설함수는 0과 1 (false / true) 혹은 그 사이의 값을 가지게 하고싶은데, linear regression에서 썼던 가설 함수를 사용하게 되면 그게 안되므로 0과 1사이 값을 가지게 할 수 있는 함수를 찾았는데

그것을 sigmoid 함수라고 하고 다음과 같이 그려진다.

sigmoid_func

sigmoid를 이용해서 가설 함수를 만든다.
$$
H(X) = \frac{1}{1+e^-W^TX}
$$
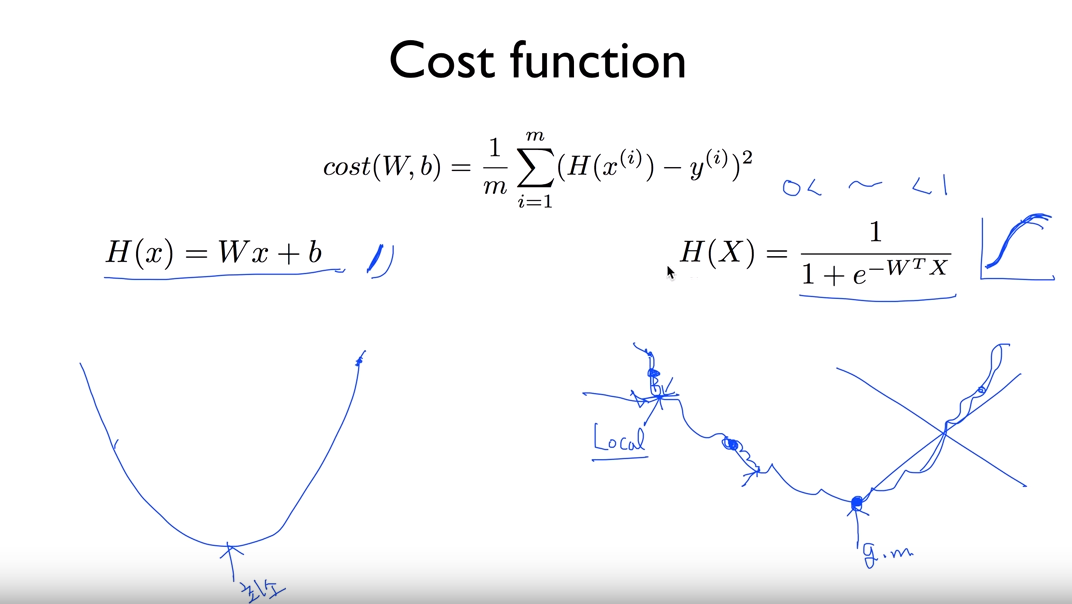
여기에 gradient descent 알고리즘을 써보려고하면

함수모양이 전에 적용했던 모양과 다르게 나와서 다음과 같이 global minimum에 도달하지 못한다.

logistic_regression_gradient_descent

그래서 cost 함수를 새로 설계해야 한다. 다음과 같이 설계를 한다.
$$
cost(W) = \frac{1}{m}\sum_{}C(H(x),y)
$$

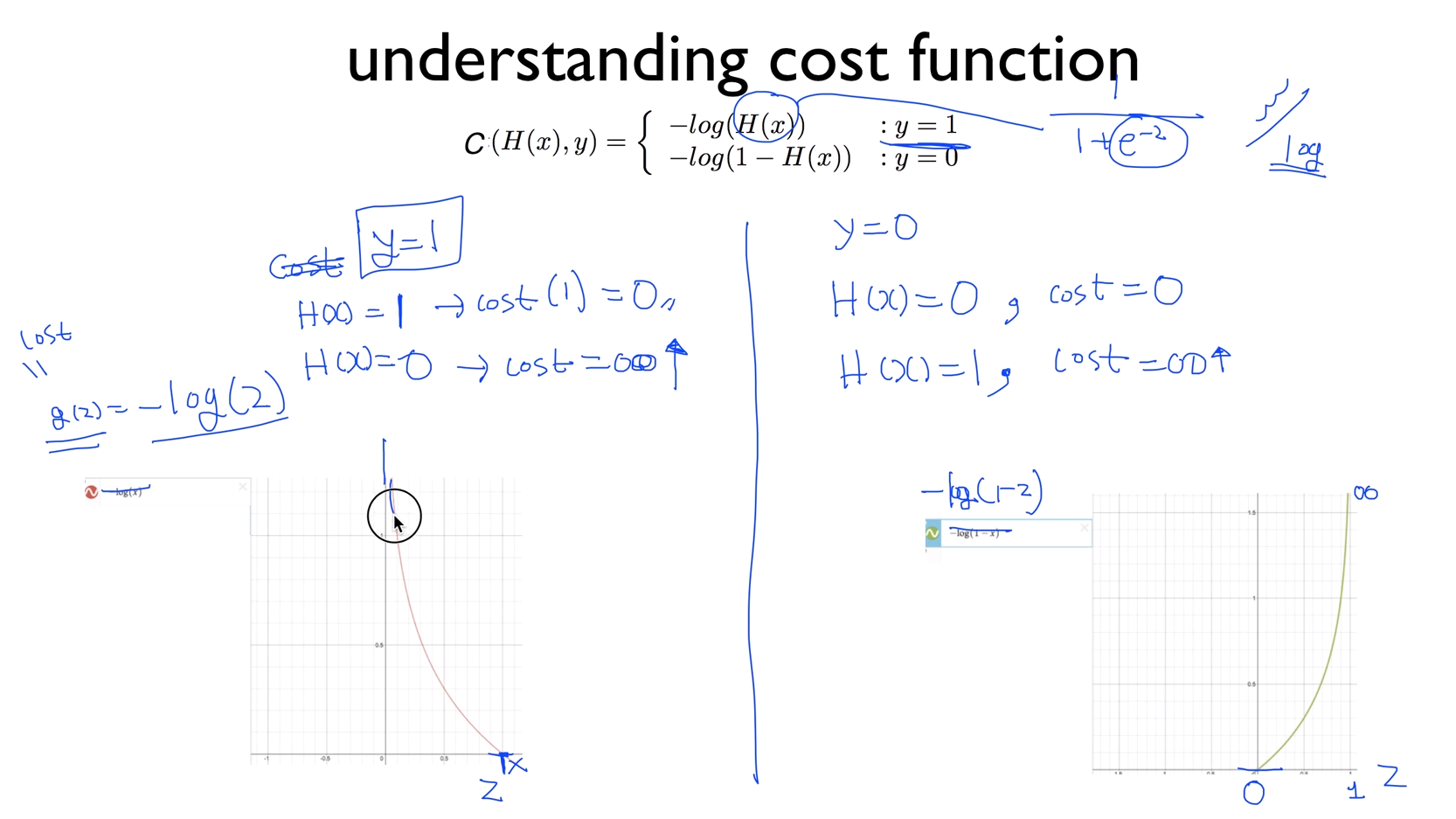
$$
C(H(x),y) = \begin{cases}-log(H(x)) && : y=1\-log(1-H(x)) && :y= 0\end{cases}
$$

위와 같이 정리해 볼수 있는데, 그래프를 보면 더 이해가 쉽다.

logistic_regression_costfunction

위 수식을 간단하게 한 term으로 정리하면 아래와 같다.

$$
C(H(x),y) = -ylog(H(x)) - (1-y)log(1-H(x))
$$
cost함수를 새로 설계했으니 gradient descent 알고리즘을 다시 적용하여 cost(W)를 minimize한다.

(Multinomial) classification

이전에는 binary classification에 대해서 배웠는데 분류대상이 3개이상의 n개로 늘어났을때는 어떻게 할까 생각해보자.

multinomial_classification

위 그림과 같이 분류대상이 A,B,C가 있고 각각 A인지 아닌지 B인지 아닌지, C인지 아닌지 분류하는 classifier를 생성하자.

multinomial_classification_2

위처럼 w1,w,2,w3의 독립된 행렬이 3개가 나오는데 이것을 아래와 같이 하나의 행렬로 합쳐서 표현해 볼 수 있다.

그러면 행렬의 곱으로 나온 값은 우리가 예측하고자 했던 “Y”(Y의 hat) 값인데 이것은

저위의 그림박스안에 “S”라고 표현한 sigmoid함수를 거치기 전에는

[ 20

, 1.0

, 0.1]

위와 같은 값일 것인데 이것을 행렬의 원소를 모두 더하면 “1”이 나오는 probability 값으로 바꾸고 싶다.

softmax

이걸 해주는 것을 softmax 라고 하고 다음의 식으로 표현이 된다.
$$
S(y_i) = \frac{e^{yi}}{\sum{j}e^{y_j}}
$$
softmax를 통해 나온 값, 위 그림에서

[0.7

0.2

0.1]

의 값에서 “야 하나만 알려줘, 예측한 값이 뭐야?” 라고 얘기하고싶다. 다른 값은 트레이닝에 의한 확률일뿐 필요가 없기 때문에.. 그래서 one hot encoding이라는 것을 통해 하나의 “1”값을 나타내고 나머지는 “0”으로 마스킹하고싶은데 tensorflow에서는 argmax라는 함수를 이용해서 이를 구현할 수 있다.

[1.0

0.0

0.0]

one hot encoding(argmax)를 쓰면 위와같이 값이 나오게 된다.

자 이제, 학습한 것과 실제값의 차이를 확인하기 위해서 cost 함수를 설계한다.

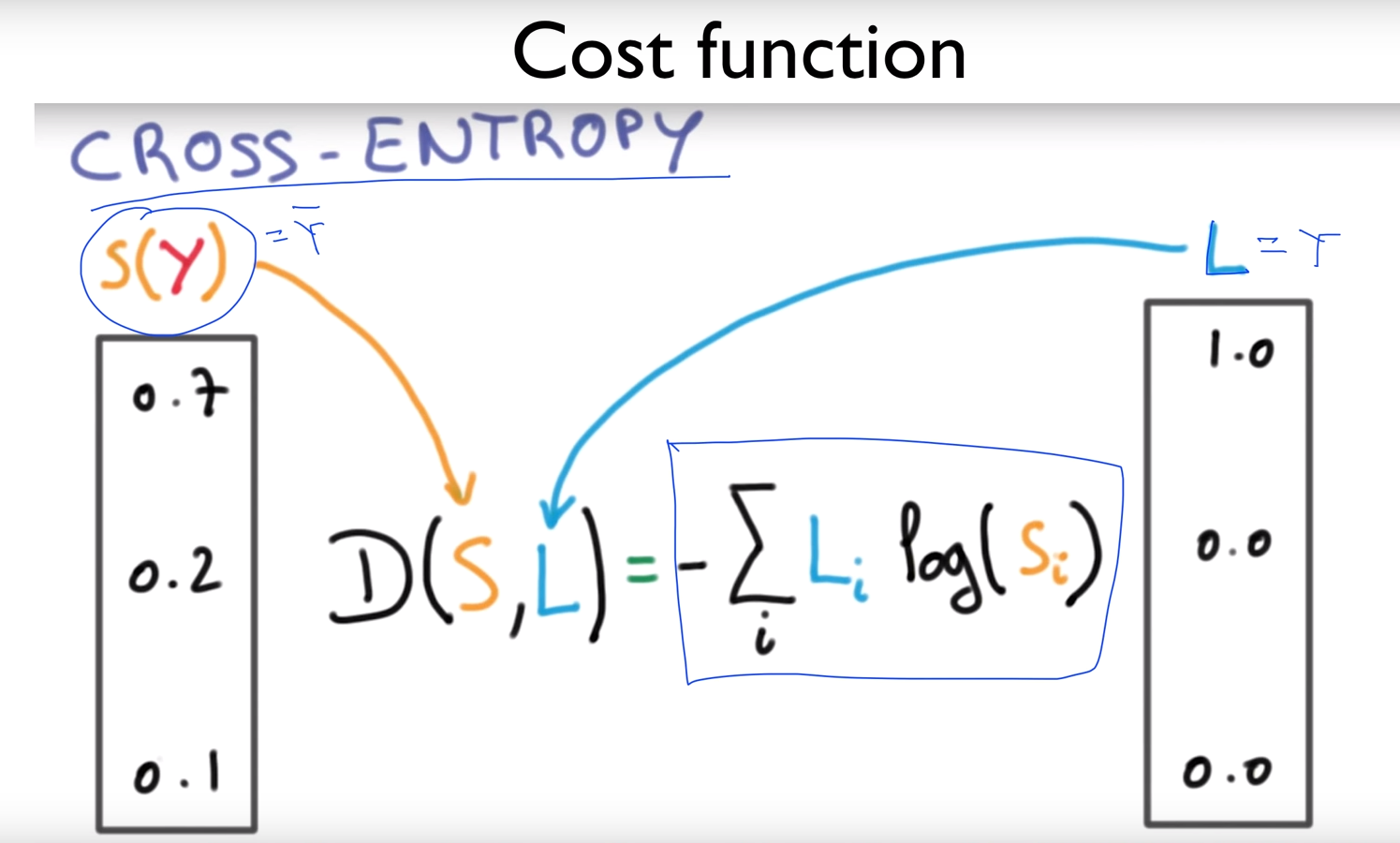
cost함수는 cross-entropy cost function이라는 것을 쓰는데

cross_entropy_cost_function

여기서 “L”은 실제 값이고 , “S”는 예측 값이다.
$$
-\sum_{i}L_ilog(\hat{y_i})
$$

$$
\sum_iL_i-log(\hat{y_i})
$$

L은 실제값이고 -log 함수는 밑의 그림의 오른쪽과 같이 그려지므로

실제값이 B일때 “B”라고 예측(초록색) 하면 0 이나오고

실제값이 B일때 “A”라고 예측(보라색) 하면 무한대로 발산한다. (계산시, element-wise 곱을 사용)

cross_entropy_cost_function_2

지금까지는 하나의 트레이닝데이터에 대해서 알아본 것이고, 여러개의 데이터셋으로 일반화 시키면

cost function은 다음과 같이 나온다.

cross_entropy_cost_function_3

N개에 대해서 평균을 구하는 것이 이제까지 해왔던 것이랑 같다.

여기서도 이전 방법에서와 마찬가지로 Gradient Descent 알고리즘을 통해서 cost를 minimize하는 방법을 사용한다.

learning rate, Overfitting, Regularization

learning rate

learning rate는 너무 작게 주면 우리가 찾고자 하는 cost 함수의 최소값을 찾는게 느리게 되고,

learning rate가 크면 발산하게 minimum 값을 못 찾고 발산(overshooting)하게 되는 경우가 생기므로,

적절하게 조정을 해야하는데 강의에서는 0.01 정도로 주기를 권장함.

gradient descent를 빠르게 하기 위한 방법

  1. standardization

    regularization_standardization

    평균을 빼고 분산으로 나눠줌.

    ​

  2. feature scaling

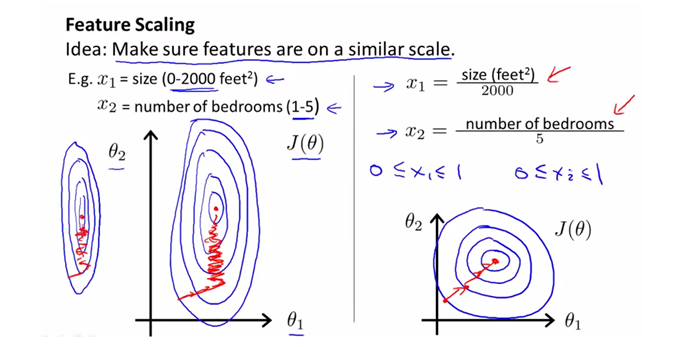
coursera_ML_feature_scaling

모든 feature를 -1<= x <= 1 사이로 만든다.

  1. mean normalization

coursera_ML_Mean_normalization

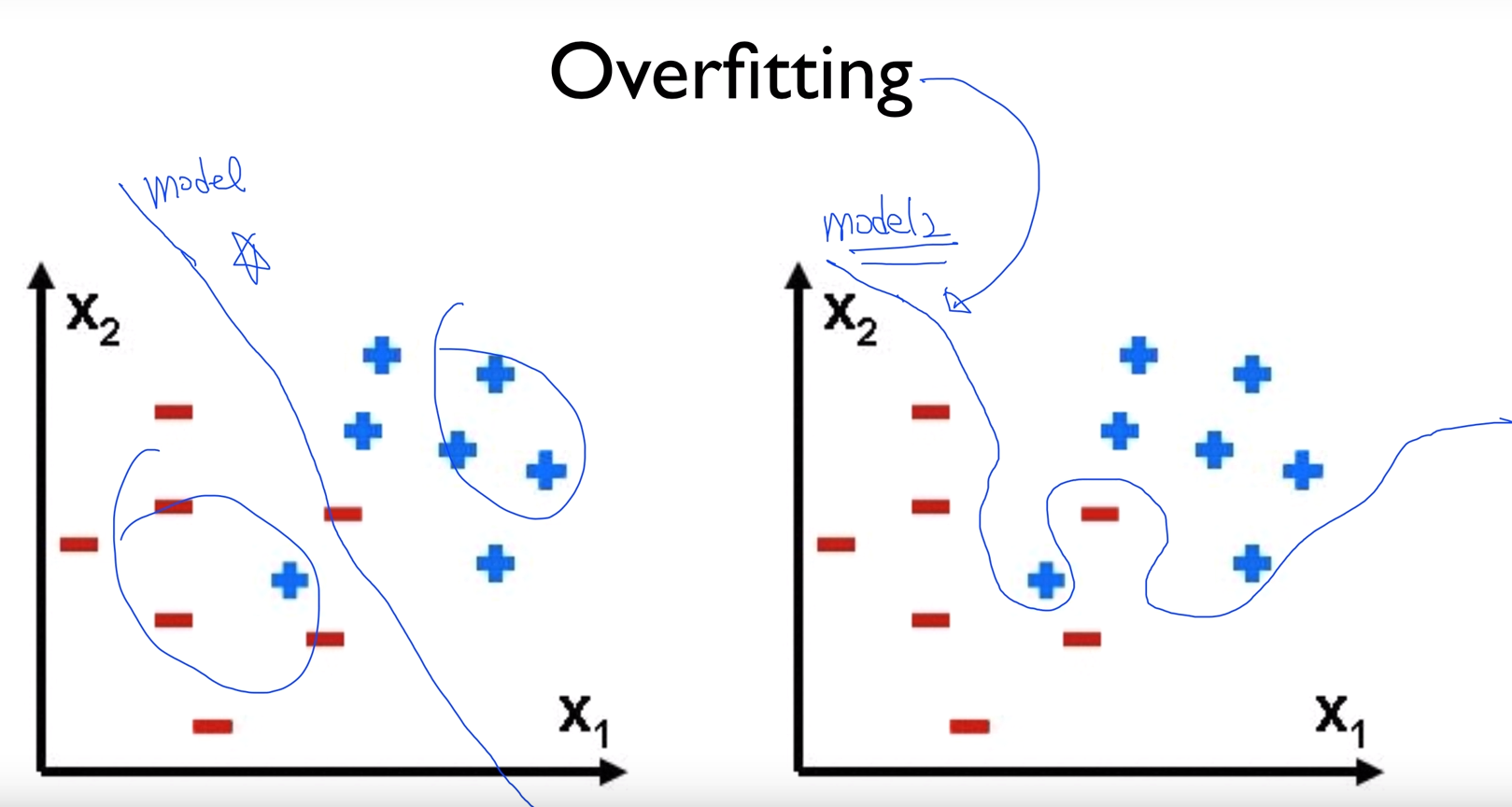
overfitting

overfitting

train data set 에 너무 잘 맞도록 학습을 진행하여 특정 데이터셋에 overfit하게 만든 것을 overftting 되었다고 한다.

overfitting을 줄이는법

  1. more training data
  2. reduce the number of features
  3. regularization

overfitting 도 문제지만 underfitting 문제 - 설계한 모델이 cost function을 최소화하는데 적합하지 않음 - 도 있다.

overfitting, underfitting을 해소하기 위해 우리는 model selection(hypothesis 선택) 부터 제대로 해야한다.

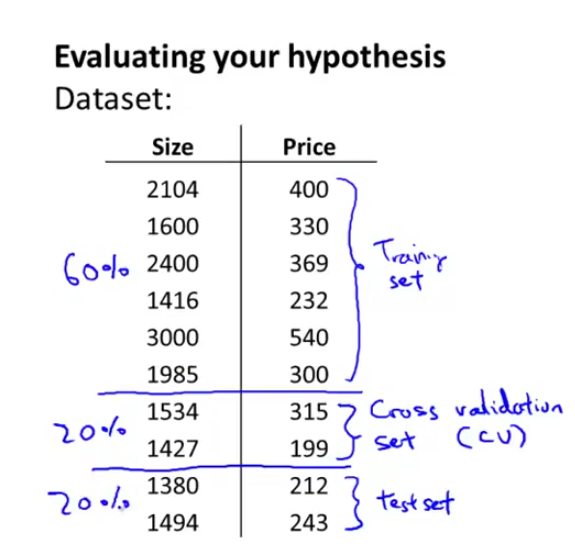
coursera에서는..

coursera_evaluate_hypothesis

위와 같이 60% 는 training set, 20%는 cross validation set, 20% 는 test set으로 사용하라고 한다.

cross validation set으로는 다음과 같은 model selection을 하는 일을 할 수 있다.

coursera_ML_model_selection

hypothesis를 degree of polynomial ( n차 다항식 ) 에 따라 n차까지 만들고 cross validation set을 이용해

cost function을 가장 작게 만들수 있는 n차 다항식을 선택한다.

선택된 hypothesis를 test set으로 선택한 데이터를 이용해 테스트한다.

이 때, 일반적으로 CV error 가 test error 보다 더 작은 값을 가지는데 선택한 모델이 CV set에 대해 fit하게 만들어져 있기 때문이다.

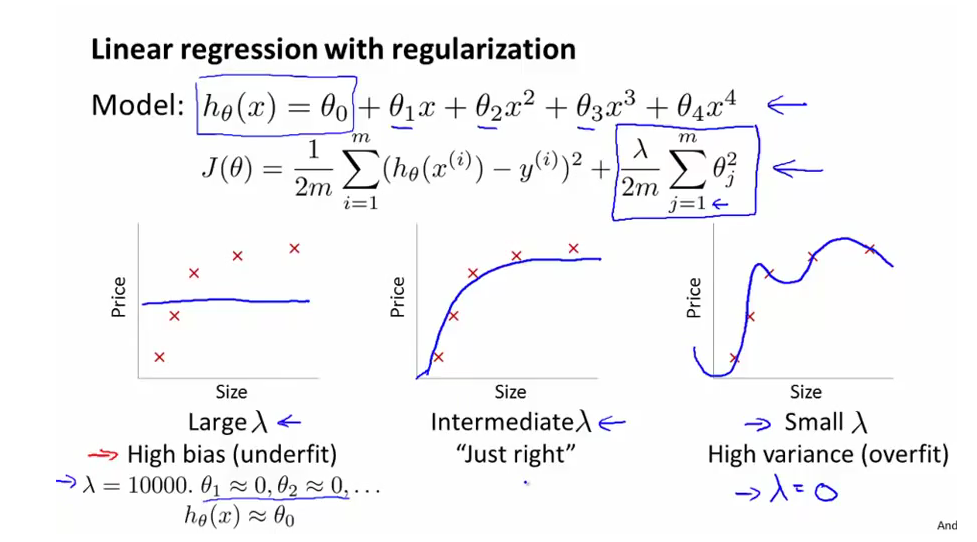
linear regression에서 overfit, underfit 문제는 bias, variance를 진단하는 문제로 생각할 수 있는데

coursera_ML_linear_regression_with_regularization

위그림 왼쪽아래가 High bias 인데 이와 같이 lamda값이 매우 클 경우에는 underfit되는 경향이 있고, lamda값이 작을 때, overfit되는 경향이 있다.

김성훈 교수님 강좌에서 보면 lamda값 조정을 통해 overfit되는 곡선을 부드럽게 이을 수 있다고 하였는데 적절한 lamda 값을 사용하면 가운데와 같이 “just right”한 함수를 얻게 될 수 있다.

위에서는 lamda값의 변화에 따른 그래프 변화를 본것이고,

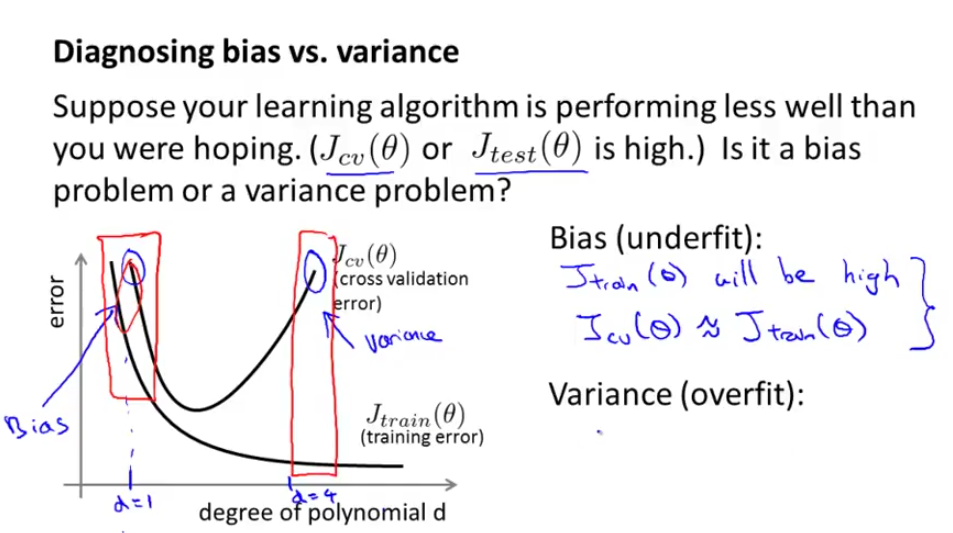
다음은 degree of polynomial에 따른 error 그래프이다.

coursera_ML_diagnosing_bias_variance

위 그림의 x축은 다항식의 차수이고, y축은 error, trainig error J 함수는 위와 같이 다항식의 차수가 늘어남에 따라 overfit 되는 경향이 있으니 줄어든다.

그리고, polynomial degree가 작고 bias가 클때 (그래프의 왼쪽 부분일때) train set, cv set 모두 큰 에러를 나타내고 있고, degree가 올라감에 따라 J(cv error)함수는 낮아지다가 어떤 임계점 이상에서는 degree가 올라감에 따라 CV error 의 J함수의 값은 커지게 된다.

그럼 어떻게 learning algorithm을 디버깅하여 예측을 잘 할 수 있을까?

coursera_debugging_learning_algorithm

위처럼 feature도 점차 증가시켜보고, polynomial feature도 점차 증가시켜보고,

lamda값도 점차적으로 증가시켜보는 방법을 통해서 learning algorithm을 디버깅할 수있다.

Share