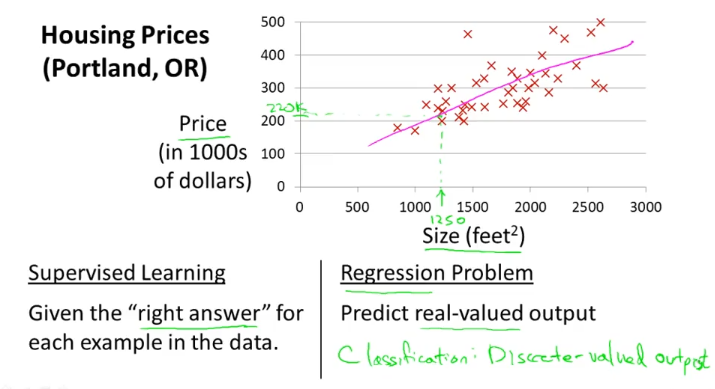
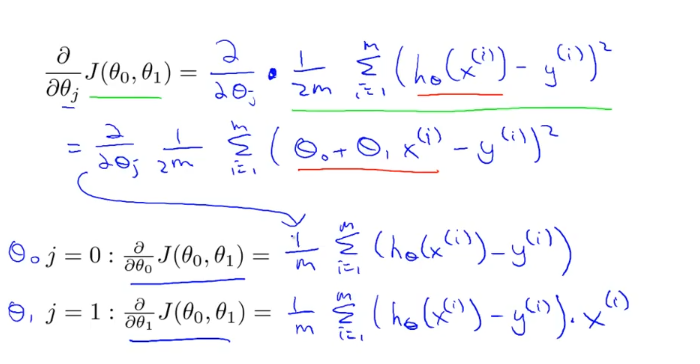위와 같이 집가격을 예측하는 문제가 있다고 하자.

이것은 “right answer” data 가 주어지는 supervised learning 이고,

또한, continuous value output을 예측하는 regression problem이다.

cost function 설계

m : training example

cost function “J”를 최소화하는 세타0, 세타1을 찾고 싶은 것.

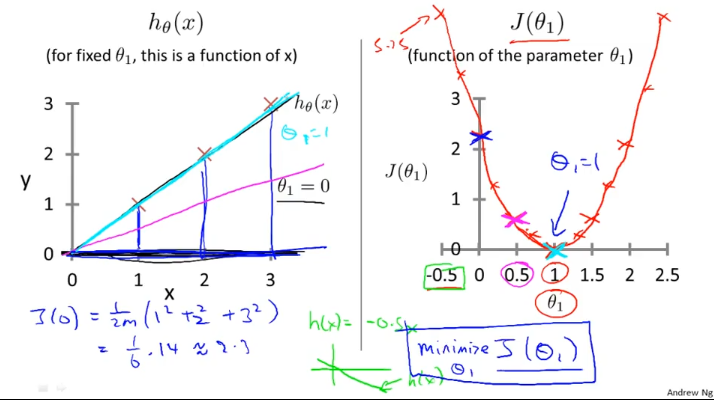
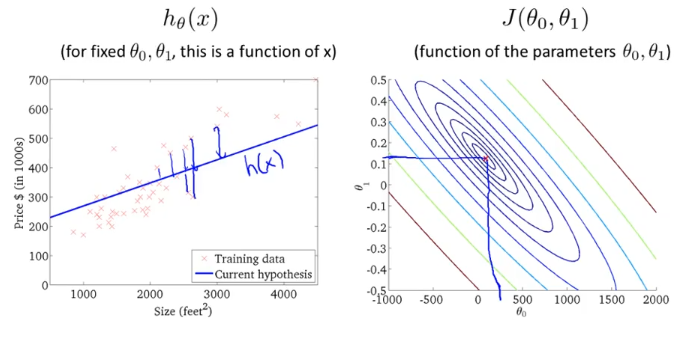
우리가 설계한 hypothesis , cost function은 다음과 같고, 이해하기 위해 세타0 = 0로 두고 생각해보자.

그렇다면 가설함수 h(x)가 세타1값의 변화에 따라 바뀌게 되고, 그에 따라 비용함수 J(세타1)도 바뀌게 되는데

비용함수는 오른쪽과 같이 그려진다. 세타1이 0.5일때 분홍색 h(x)선이 그려지고 그때 J(세타1) 값은 오른쪽에 분홍색 x 표시한 것과 같음.

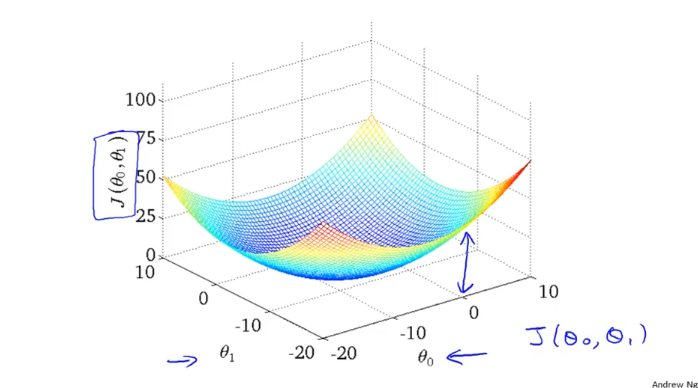
간소화한 비용함수를 봤으니 원래 세타0, 세타1의 두개의 파라미터를 가지는 함수로 돌아가보자.

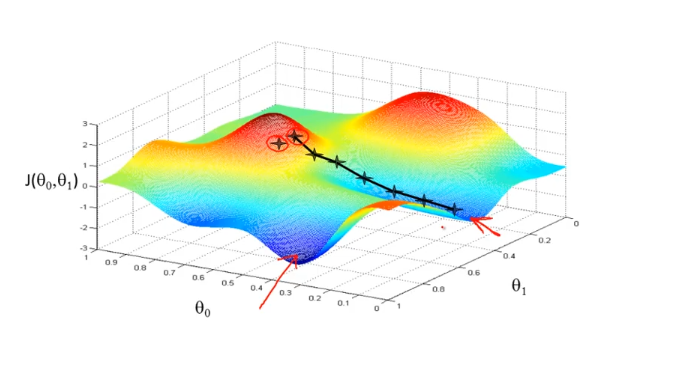
위와같이 3차원의 형태로 나타나게 된다. 밑면에서의 높이가 J(세타0, 세타1)의 값 = cost가 된다.

하지만 위와같은 3차원그림보다 직관적으로 이해하기 쉽게 다음과 같이 표현할것이다.

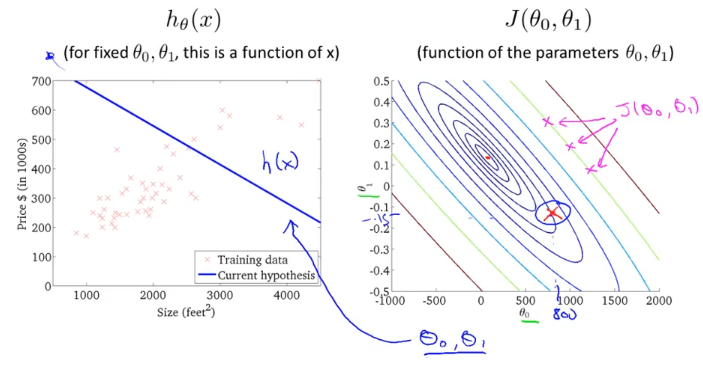
오른쪽 그림을 “contour plot” 이라고 부르는데 분홍색으로 표시한 “x”점들의 J 값은 모두 같다. 이전 그림을 위에서 본 단면도같은 것이다. 그럼 비용함수 J의 특정 점에 해당하는 h(x)를 찾아볼건데,

샘플로 세타0가 800이고 세타1이 -0.15 정도 될때 h(x)는 왼쪽 그림과 같이 나타나게 된다.

최소값과 근접한 J는 안쪽 원에 있고, 이것의 h(x)는 아래왼쪽 그림과 같다.

그런데 우리가 하기 싫은것은 점을 찍어가면서 수작업으로 최소가 되는 J값과 그에 따른 h(x)를 찾는 것이 아니다.

파라미터가 그림을 그릴수 없을 정도로 많아지면 시각화도 할 수 없을 것이고, 그래서 수작업으로 최소값 J와 그에 따른 h(x)를 찾을 수 없을것이다. 그래서 우리는 알고리즘을 통해 이작업을 자동화할 것이다.

Gradient Descent

Gradient(경사) Descent(하강) 알고리즘은 말그대로 위와 같은 그림의 산이 있다고 하면 그 산에서 주위를 둘러보면서 내려갈 곳을 찾고 한스텝씩 내려가는 알고리즘이다.

그런데 위 그림에서 보듯이 시작하는 점이 다르게 된다면 “빨간색 화살표로 표시한” 다른 지점(local minimum) 에 도착할 수 도 있다.

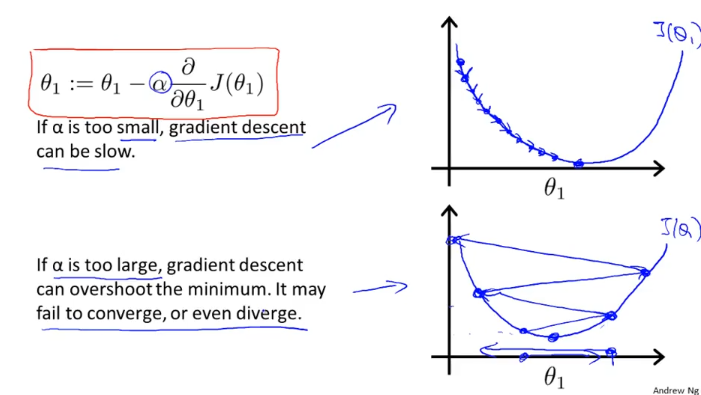
Gradient decent algorithm을 수학적으로 표현하면 다음과 같다.

위에 alpha는 learning rate를 표시하고 경사면으로 얼마만큼 내려갈지를 표현하는것이다.

유의해야할 점은 세타0와 세타1을 simultaneous update를 해야한다는 것이다. 오른쪽아래 식처럼 업데이트를 하면 update된 세타0값이 세타1을 계산할 때 들어가므로 적절하지 않다.

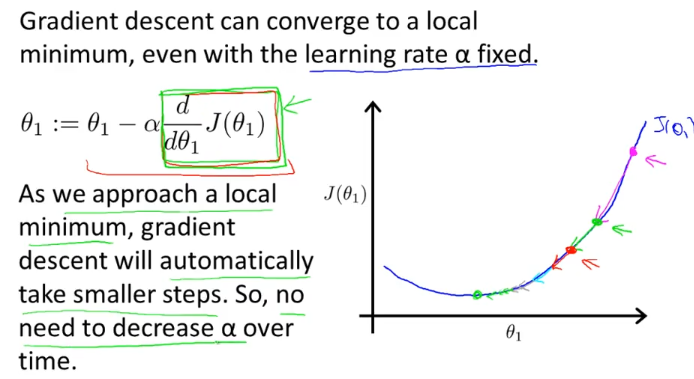
다음은 learning rate alpha 값에 따라서 세타1이 어떻게 변하는지 나타낸 그림이다.

alpha가 작으면 small step으로 이동하고 alpha가 너무 크면 converge에 실패 할 수 있고, 오히려 발산 할수도 있다. 만약 미분값이 0이나오면 그다음엔 어떻게 될까? - step이 계속 진행되지 않고 그자리에 머물게 된다.

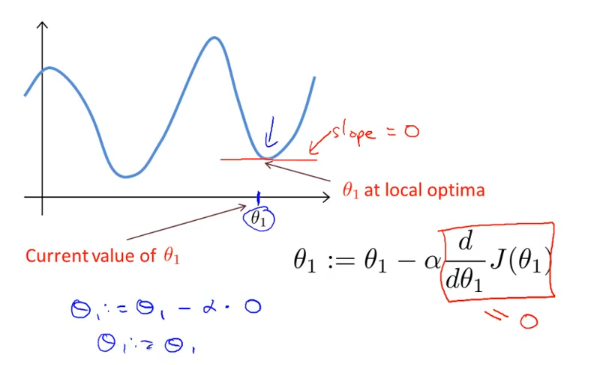
다음 그림이 그 예제 중에 하나인데, global minimum에 도착하지 못하는 경우다.

만약 그림의 오른쪽 점에서 경사 하강 알고리즘을 시작했다면 미분값이 0이 될때 세타1은 더이상 업데이트 되지않는다.

경사하강 알고리즘은 learning rate alpha가 고정되어있어도, 위의 초록색 네모박스로 표시한 미분값이 점점 작아짐에 따라 점점 small step으로 경사를 내려가게 된다.

이제 우리가 할 것은 gradient descent algorithm을 linear regression model의 cost function에 적용해보는 것이다.

위 왼쪽의 네모박스에 있는 편미분을 해보자

세타0와 세타1에 대해 편미분한 식은 위와 같이 도출된다. (식을 유도하는 것은 몰라도된다고 한다.)

이제 gradient descent algorithm에서 배웠듯 위 두 세타0와 세타1을 simultaneously update를 하면된다!

그림을 통해 어떻게 동작할것인지 살펴보자.

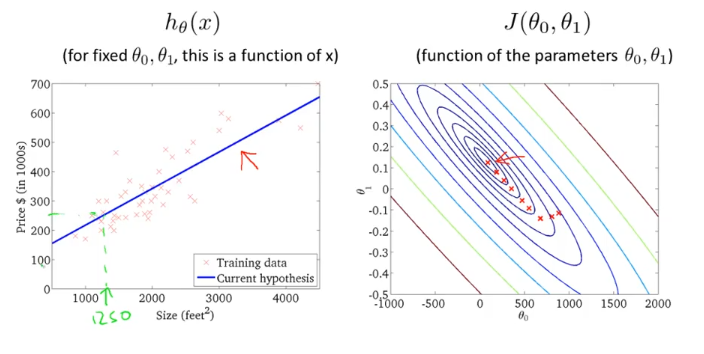
세타0 = 900, 세타1=-0.15 를 시작점으로 gradient descent algorithm을 적용한다고 하자. 그러면 경사면을 내려감에따라 h(x)가 변화하게 될것이고, 결국 global minimum에 도착하게 될 것이다.

그러면 이때 얻은 h(x)를 이용해 새로운 데이터가 들어와도, 사이즈에 따른 아파트 가격을 예측할 수 있다.