multivariate Linear regression

지금까지 feature가 하나인 linear regression문제를 풀었고, 이제 feature가 여러개일때에 linear regression 문제를 풀어보도록 한다.

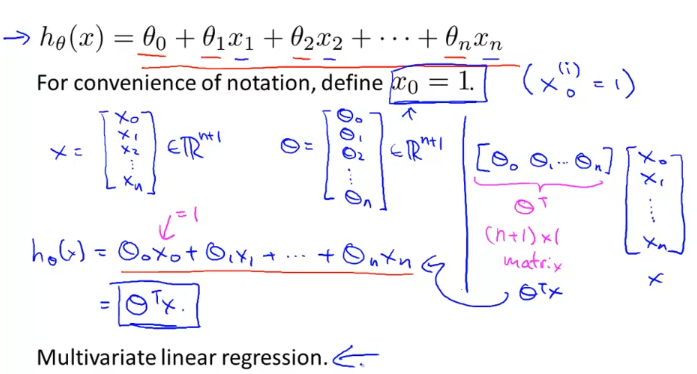
가설함수 h(x)는 위와 같이 나타낼 수 있고, 이때 x0 = 1이라고 정하면 벡터 X와 벡터 세타는 위와 같이 정의할 수 있고, h(x)는 간단하게 “세타 transpose X”로 표현 할 수 있다.

이제 multivariate linear regression의 cost function에 대해서 알아보자.

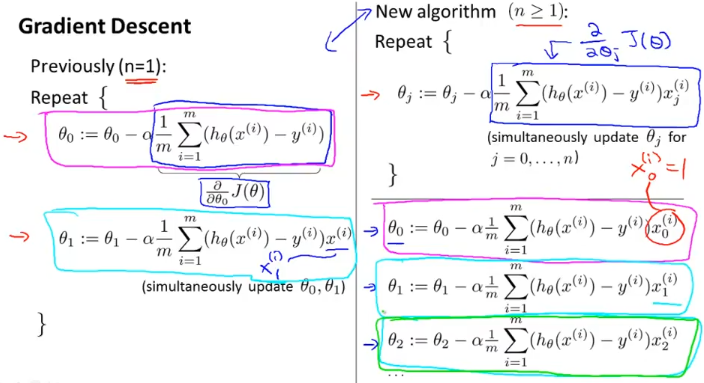
위와 같은 식으로 나타나게 되고,

n=1일때와는, 세타0일때 x0(i)를 곱해주고, 세타1일때 x1(i)를 곱해주는 것만 다르다. (그부분은 편미분 적용하는 식이니까)

feature scailing

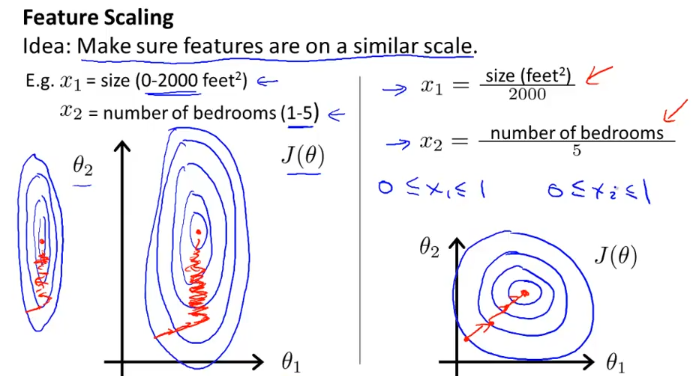
x1 과 x2이 가지는 값의 범위차가 크면 위의 왼쪽 그래프와 같은 contour plot 이 나올 수가있다. 그럴 경우에 그림에서 보듯 gradient descent가 어디로 내려갈지를 제대로 찾지 못하고 이쪽 저쪽 내려가며 헤매는 경우를 겪을 수 있는데 이를 해소하기 위하여 feature scaling이라는 방법을 쓰는데 오른쪽과 같이

각 범위의 최대값으로 나눠줘서

x1, x2를 0과 1사이의 값으로 만들어주면 contour plot이 오른쪽과 같이 된다.

위와 같이 모든 feature가 대략 -1에서 1사이의 값을 가지도록 설정을 해야 gradient descent algorithm이 잘 돌아간다. 위 그림에서 x표로 표시한 feature 처럼 값의 범위가 너무 벗어나 있으면 feature scaling을 통해 값을 조정하자.

feature scaling - mean normalization

feature scaling의 한 방법으로 mean normalization이라는 것을 쓸수가 있는데,

위와 같이

x1에 (x -u1) / s1 을 하는 것이다. (x2, x3도 같은…식으로)

u1 : train set 에 있는 x1의 평균값

s1 : max - min (범위), or 분산(standard deviation)을 써도 된다.

learning rate

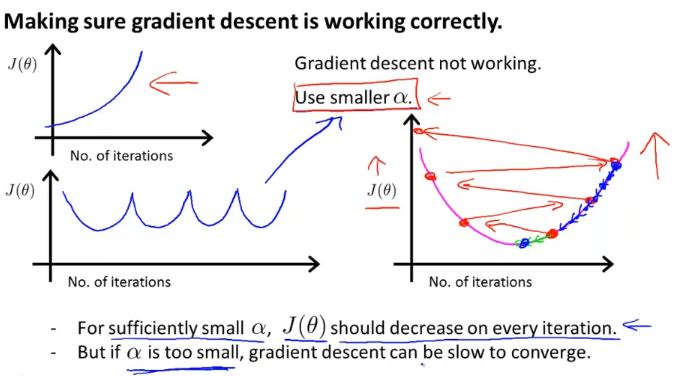
위 왼쪽 그래프의 x축은 gradient descent algorithm 반복횟수 (No. of iteration)

y축은 cost function J의 값이다.

cost function J는 계속 해서 감소하지만 어느 순간(300~ 400 반복사이)부터 거의 감소하지 않고 일정한 수준을 유지하게 된다.

그래서 주로 왼쪽처럼 그래프를 그려서 converge 하는지 확인하는데,

이를 자동화할 수 있는 방법으로 작은 epsilon 값을 하나 정해서 각 iteration마다 정한 epsilon 값보다 떨어지면 converge했다고 정할 수 있다.

그런데, 이 epsilon 값도 정하기가 어려우므로 보통 왼쪽의 그래프를 그려서 확인하는 방법을 쓴다.

cost function J가 왼쪽 그래프와 같다면 learning rate가 크다는 얘기이고, 오른쪽 그래프처럼 세타값이 업데이트 되면서 발산하게 된다 이럴때는 alpha값을 더 작게 해준다.

alpha 값이 너무 작으면 gradient descent가 너무 느리므로 적절한 값을 넣어주는 것이 중요하다.

Andrew Ng 교수가 할때는

0.001, 0.003, 0.01 , 0.03 , 0.1 , 0.3, 1

이렇게 약 3배정도씩 증가시키면서, 가장 큰 learning rate의 가장 작은 값과 큰 값을 얻은 다음에

가장 큰값을 선택하거나 가장 큰값보다 약간 작은값을 learning rate로 선정한다고 한다.

features and polynomial regression

때로는 feature간의 연산으로 하나의 feature를 만들어서 사용할수 있다. 다음 예를 보자.

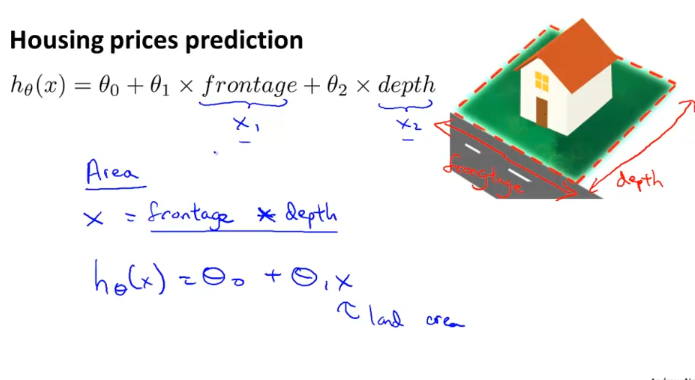
위와 같이 집값을 예측하는 모델을 만든다고 할 때에, 대지의 가로 세로를 각각 feature로 사용하는 것보다 단순하게 area = 가로 * 세로 로 사용할 수 있다.

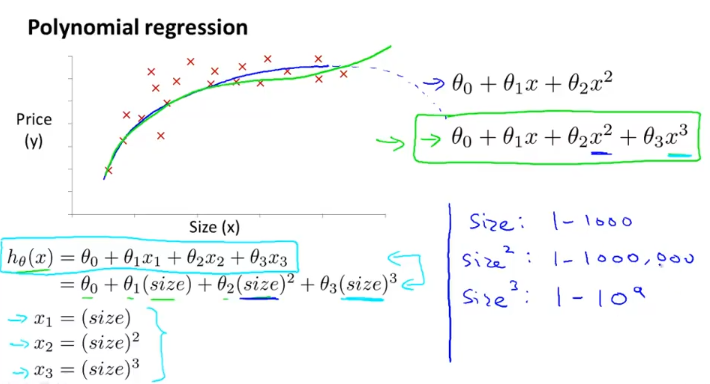
그렇게 feature를 하나로 한정시키고 이에 대한 h(x)를 위와 같이 3차함수로 설정하자. 2차함수로 설정시 올라갔다가 다시 내려오는 형태가 되므로 3차함수로 정했다.

3차 함수는 왼쪽 아래처럼 나오게 되므로 각 항의 값 범위(size, size제곱, size세제곱)가 크므로 feature scaling을 통해 gradient descent가 잘 돌아가도록 해야한다.

3차 함수로 하지않고 루트 함수로 가설함수를 세우면 train data에 더 fit하게 할 수 있다.

feature를 우리가 정하지않고 data를 보고 자동적으로 feautre를 select 할수 있는 알고리즘도 있는데, 그것은 다음에 배우도록 한다. 여기서는 다항함수나, 루트함수등으로 데이터를 표현할 수도 있다는 것을 살펴보았다.