logistic regression에 관련한 h(x), cost function , multiclass Classification,
Gradient Descent 외에 다른 알고리즘을 쓰는 부분은 다음 링크 or “모두의 딥러닝” 정리 노트로 대신한다.
https://1ambda.github.io/data-analysis/machine-learning-week-3/
그 다음부터 정리.
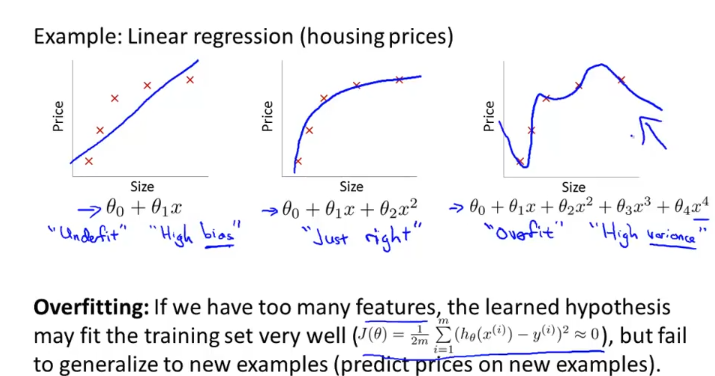
The Problem of Overfitting
위 그림의 왼쪽 처럼 평평한 가설함수로 인해 train data set에도 충분히 맞지않은 것을 “underfit” 이라고 하고, “High bias”라고 한다.
반면, 오른쪽처럼 거의 모든 train data set에서 잘 들어맞지만, 새로운 data에 대해서는 잘 맞추지 못하는 상황을 우리는 “overfit” 되었다고 하고, “High variance”라고 한다.
가운데처럼 train data set에 적절히 맞고 새로운 data도 적절하게 맞추는 h(x)가 우리가 찾고자 하는 것이다.
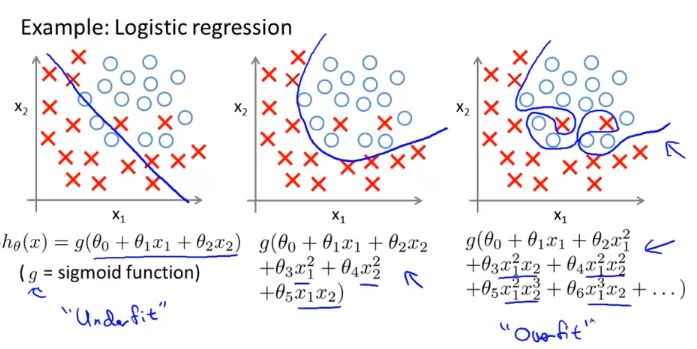
logistic regression에서도 overfit, underfit 현상이 나타날 수 있는데 다음과 같다.
linear regression과 마찬가지로 위와 같이 data set이 주어졌을때 평평하게 선형으로 예측한 것은 “underfit”
심하게 구불구불하여 train data set에는 잘 맞지만 새로운 data는 잘 맞추지 못하는 것을 “overfit”이라고 한다.
이러한 overfitting을 처리하는 방법은 위와 같다.
feature의 개수를 줄인다.
: 어떠한 feature를 남길지 직접 선택한다.
: 어떠한 model을 쓸지 고르는 알고리즘 (Model selection algorithm)을 사용한다.
Regularization
: 많은 파라미터를 가지고 있는데 그것이 값(y)를 예측하는데에 도움이 된다고 하면,
모든 feature를 살려놓고, parameter theta의 규모/값을 줄이는 방법이 있겠다. - later course에서 살펴보자.
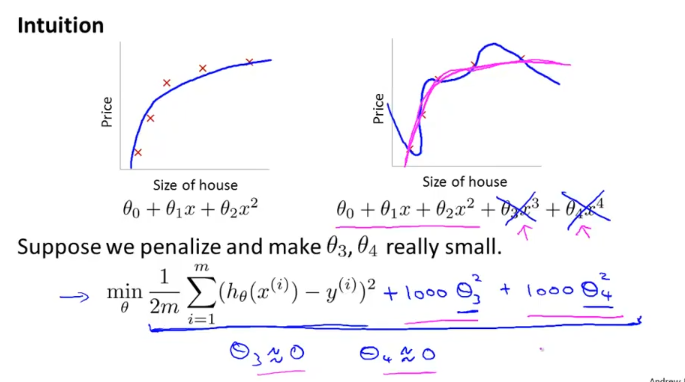
Cost Function
위 그림의 식과 같이 cost function을 세우면 theta3, theta4를 0에 가깝게 하는것이 cost function의 값을 줄일 수 있는 방법이고, 그렇게 되면 곡선이 펴져서 마치 quadratic function 처럼 보이게 된다.
theta3, theta4를 0으로 가깝게 만든 전장의 내용을 일반화 시켜보면
parameter가 작은(규모/값) 경우에
- “simpler” 한 가설함수
- overfitting될 가능성이 적음
을 알 수 가있다.
Housing price를 예측하는 우리의 문제에 대입해보면 feature가 100개나 되는데, 어떤 parameter가 y를 예측하는데에 얼마나 영향을 끼칠지 우리는 모른다.
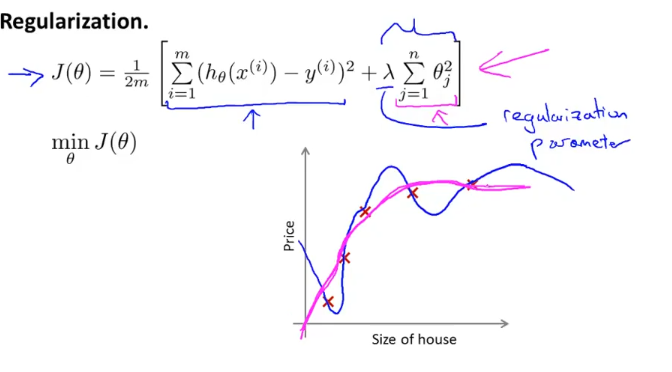
그래서 cost function에 regularization term을 붙여서 각각의 파라미터 theta 의 제곱에 lamda 값을 붙여서 cost function을 표현한다. (theta0를 포함하는 것은 결과에 큰 영향없으므로 i = 1부터 시작함) 이렇게하면 모든 parameter theta의 값을 줄어들게 할수가 있다.
전장에서 cost function을 위와 같이 만들었다. 우리는
앞의 term( h(x) -y)의 제곱 )과 뒤의 term (regularization)을 모두 최소화 해야하기 때문에
train data에 잘 맞으면서, parameter theta의 영향은 줄어든 cost function을 설계했다.
regularization에도 lamda값이 너무 크면 모든 parameter가 0에 수렴하여 “underfit” 현상이 나타날 수 있다.
Regularized Linear Regression
이 앞에서 Linear Regression에 대한 regularized cost function을 만들어 보았다.
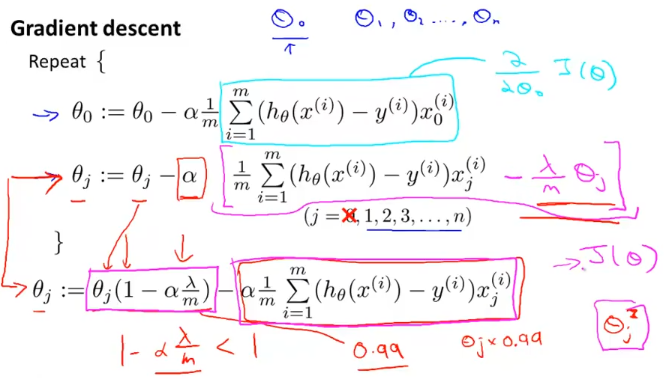
이를 토대로 gradient descent 알고리즘도 적용해 볼텐데 다음과 같다.
theta 0은 regularization term에 들어가지 않았으니 따로 빼서 계산하고,
theta (1~n) 까지는 빨간색 화살표의 식으로 나타낸다. 그 식을 정리하면 맨 밑에 표현한 식으로 나타낼 수 있는데
$$
1 - \alpha\frac{\lambda}{m} < 1
$$
위와 같이 first term의 식을 보면 1보다 작으므로 parameter theta 를 조금씩 0으로 가깝게 만든다.
second term을 보면 이는 이전에 우리가 세운 gradient descent 알고리즘과 같다.
normal equation
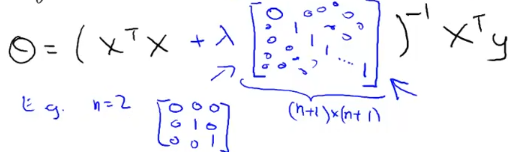
normal equation에 regularization term을 적용해보자.
그러면 위와 같은 식으로 나타나게 되고 n = 2 일때 3*3행렬인데
theta 0는 제외하니까 그것만 0으로 놔두고, 위와 같이 단위 행렬(identical matrix, unit matrix) 과 비슷한 형태로 나타나게 된다.
lamda > 0 이면, 위의 역행렬에 쌓인 식은 non-invertible함을 증명할수 있다. 즉, regularization을 통해 non-invertible 문제도 해결할 수 있다.
Regularized Logistic Regression
Logistic Regression도 Linear regression과 같이 theta 0, theta (1~n) 을 나눠서 생각하는 방식으로 gradient descent를 적용할 수가있고, 다음과 같이 cost function을 구현한다.