Evaluating a Learning Algorithm

Deciding What to Try Next

여러가지 문제로 당신의 머신러닝 시스템이 예측을 제대로 못할수가 있다. 앞으로는 여러분들의 삽질(?)을 줄일 수 있는 테크닉들에 대해서 알아볼 것이다.

위 그림의 아래에 적은 리스트 처럼,

get more training example을 할수도 있다. 그런데, 아무리 많은 training 데이터를 집어넣어도 새 값에 대한 예측은 제대로 못할수가 있다. 그 밖에 다른 방법들도 마찬가지… 어떻게 적절하게 변수들(feature, lamda, polynomial feature 등..) 조절할 것인가에 대한 것을 이번주에 알아보기로한다.

Evaluating a Hypothesis

모든 dataset을 train data set으로 사용하면 마치 답을 알고 시험을 치는 것처럼 train data set에 “overfit” 될 수 있다. 이 것을 해소하기 위해 다음 그림처럼 data set의 70%는 training set, 30%는 test set으로 나누는 방법을 생각해 볼 수 있다.

linear regression은 위의 과정처럼

1. train data set으로 학습시켜 cost function J(theta)를 최소화시키는 theta 값을 찾고
2. test data set 으로 cost function J(theta)를 평가한다.

logistic regression은 어떨까?

logistic regression도 linear regression과 같은 방법을 사용할 수 있다.

아니면, misclassification error 를 이용해도 된다. y = 0 일때 h(x) < 0.5 이어야 하고, y = 1 일때 h(x) => 0.5 이어야 하기 때문에 엇갈리게 나온 경우 err 함수에서 1 을 리턴해, 이 값을 모두 합한 뒤 전체 테스트 셋의 숫자로 나누면 테스트 에러를 구할 수 있다.

Model Selection and Train/Validation/Test Sets

“overfitting”에 대해서 알아보았다. 우리는 “overfitting”을 피하고, 값을 잘 예측할 수 있는 모델을 원하는데 어떻게 그런 모델을 고를 수 있을까? 이에 대해서 알아보자.

1 ~ 10차까지의 차수를 가지는 가설함수 10개를 만들고, 각각 test data set으로 돌려 cost function J값을 알아낸다. 이때, 가장작은 cost function 값을 가지는 model의 차수를 선택했더니 예제에서 처럼 5차 다항식이 나왔다고 하자. 그런데, 이 모델은 test set에 “fit”하게 선택되었으므로 새로운 example이 나오게 되면 제대로 예측하지 못할 것 같다.

그래서 다음의 방법을 이용한다.

이전의 방법과는 다르게 전체 data set의 60%는 training set, 20%는 cross validation set, 20%는 test set으로 한다.

그러면 위에서 test data set으로 했던 model selection 과정을 cross validation set으로 똑같이 한다.

그래서 봤더니 4차 다항식이 선택이 됐고, 이 선택된 다항식은 이전처럼 test data set에 “overfit”되지 않은 것이므로, 이것을 test set에 적용해보면 일반적인 에러값에 대한 추정치를 얻을 수가 있다.

Bias vs. Variance

모델이 잘 돌아가지 않을 때, 많은 경우 high bias problem 이거나 high variance problem, 즉 “underfit” or “overfit” problem이다. 이럴때 내 모델이 어떤경우인지 판단하고 그것에 맞게 모델에 고쳐나가는 것은 매우 중요한 일이므로 이것에 대해 알아보자.

Dignosing Bias vs. Variance

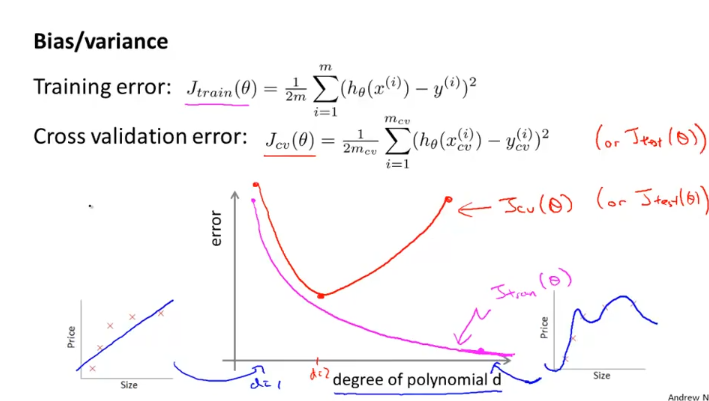
다항식의 차수가 늘어 날수록 train data set에 더 알맞는 h(x)를 찾을 수가 있다 그래서, 위의 분홍색 그래프와 같은 형태가 나오게 되고,

cross validation set은 차수가 작으면 “underfit”(High Bias) 때문에 error가 많아지고, 특정 차수까지 에러가 감소하다가, 특정 차수 이후부터 train data set에 “overfit”된 모델(High variance)때문에 error(cost function J)가 점점 많아지게 된다.

High Bias (underfit)일 때는, J_train(theta)와 J_cv(theta)가 거의 비슷하게 높은데,

High Variance(overfit)일 때는, J_train(theta)는 낮은데, J_cv(theta)는 이와 비교하여 매우 크게 된다.

Regularization and Bias/Variance

regularization이 “overfit”된 모델 문제를 고칠 수 있다고 얘기했었다.

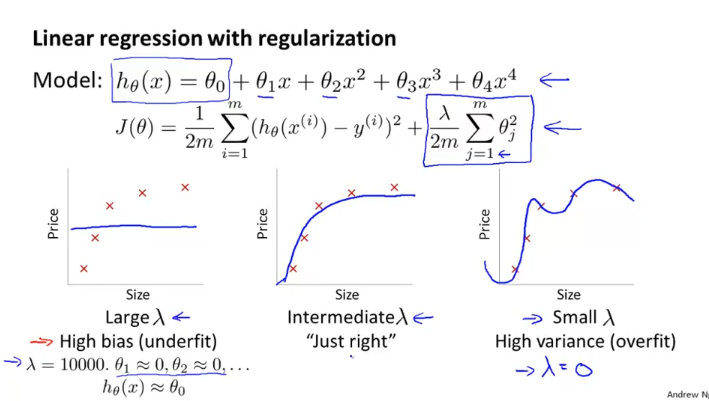
위 그림처럼 lamda가 크면 High bias(underfit)이 되고 , lamda가 작으면 High variance(overfit)이 된다. 가운데 그래프처럼 적절한 lamda값을 찾는 것이 우리가 하고 싶은 것인데 어떻게 하면 자동으로 lamda 값을 찾을 수 있을까?

위의 과정은 아래의 내용으로 정리한다.

1. Create a list of lambdas (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});
2. Create a set of models with different degrees or any other variants.
3. Iterate through the λs and for each λ go through all the models to learn some Θ.
4. Compute the cross validation error using the learned Θ (computed with λ) on the JCV(Θ) without regularization or λ = 0.
5. Select the best combo that produces the lowest error on the cross validation set.
6. Using the best combo Θ and λ, apply it on Jtest(Θ) to see if it has a good generalization of the problem.

Learning curves

learning curve는 당신의 모델이 High bias , High variance problem등의 겪고있지않은지, 잘돌아가는지 확인하고 있을때 활용할 수 있다.

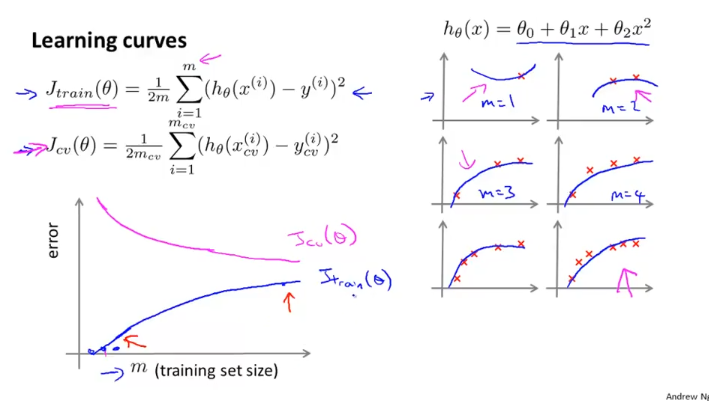
training set size가 작으면 J_train(Θ)는 주어진 data 에 비슷하게 맞출 수 있고, training set size가 늘어남에 따라 error가 커진다.

반면에, J_cv(Θ)는 train set size가 작으면 error가 커지고, training set size가 커짐에 따라 error가 작아지게 된다.

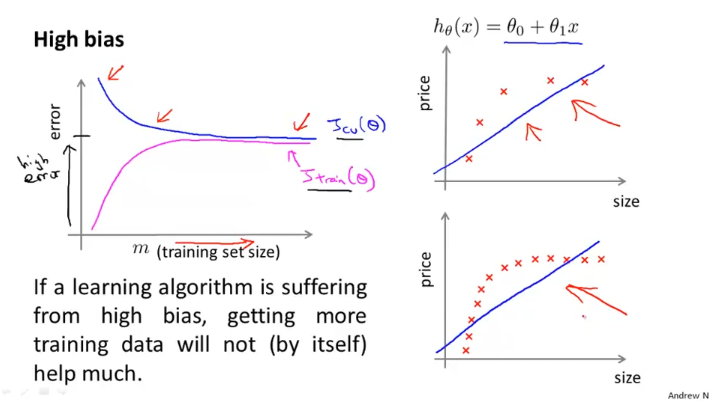
위그림처럼 설계한 모델이 high bias problem을 겪고 있다면 training set size를 증가시켜도 error는 비슷하게 나올 것이다. data set을 잘 예측하지 못하므로, error율은 J_train과 J_cv 모두 상대적으로 높을 것이다.

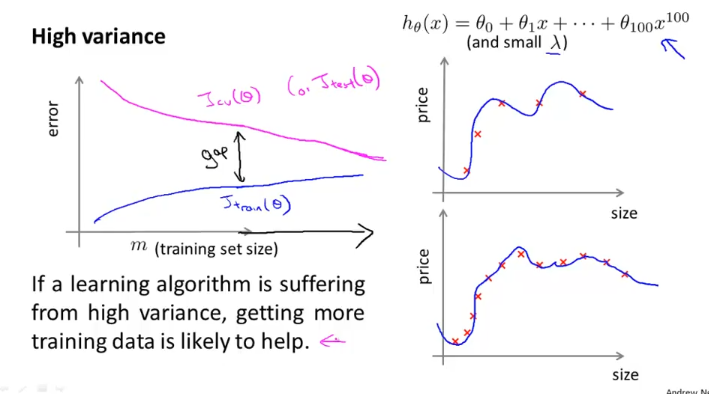
반면에 High variance 일때는 J_train과 J_cv의 gap이 크다.

하지만 training set size를 아주 많이 증가 시키면 어떨까? training set size 증가함에 따라서 위 그림과 같이 J_train의 error율은 조금씩 높아지고, J_cv의 error율은 점점 낮아진다. (J_test도 마찬가지)

Error Analysis

Recommend approach

• 심플한 알고리즘부터 시작해라. 그리고 cv data 로 테스트해봐라.
• learning curve를 그려봐라
• Error analysis를 해라.
  • CV data set에서 수동으로 example을 검사해봐라 . spam filter의 경우에 spam을 잘 못 걸러낸 경우에 대해서 검사해본다. 어떤 항목에서 에러가 발생했는지 체계적으로 검사해라.

Error Analysis example을 살펴보자.

CV data set이 500개인데 100개의 email을 spam 처리를 못했다고하면,

1. 그 data set에서 error를 category로 나눠서 살펴본다.
2. 어떤 feature가 classify를 잘 할 수 있는지 생각해본다.

그리고 수식 평가를 해본다.

discount / discounting / discounted 이런 단어들을 같은 단어라고 치고 있는가? 를 보고 이를 적용/비적용하여 CV error를 평가해본다.

With Stemming(어근(?)평가) : 3%

대문자, 소문자 구분 : 3.2 %

가 나왔다면 대소문자 구분은 크게 영향을 미치지 않는다고 치고, 더 중요한 stemming에 집중 할 수 있다.

한줄요약 :

quick and dirty application을 만들어서 빨리 해보고, 어떤 error 에 집중할 것인지 파악하여 그것에 집중하라.

Handling Skewed Data

Error Metrics for Skewed Classes

이제 아주 작은 확률로 일어나는 일에 대해서 classify 하는 알고리즘을 풀어보자.

암 환자를 가려내는 알고리즘을 짰는데 test set에서 겨우 1% 에러만 발견되었다. 제대로 예측한 건가??

아무도 암환자가 아니라고 리턴하는 알고리즘을 만들면 0.5%에러만 발견 된다면, 즉, 암환자가 0.5%정도 밖에 안되는 문제라면 제대로 예측하지 못한거다.

그래서 이러한 문제를 평가하기 위해 Precision / Recall 이라는 새로운 개념을 가져온다.

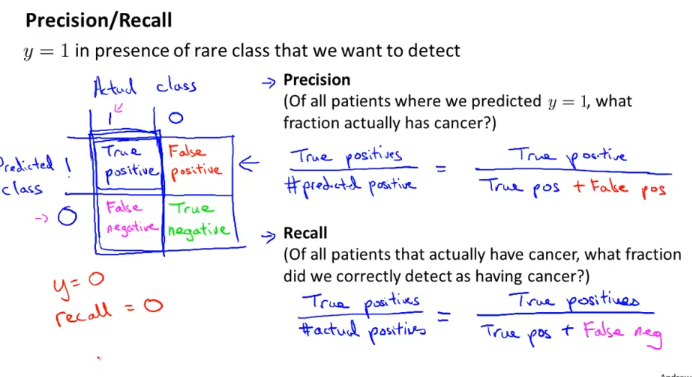
Precision(정확도) : 우리가 암이라고 생각한 환자중에서 실제로 암인사람 몇명?

Recall(재현율) : 암을 가지고 있는 사람 중에서 우리가 실제로 찾아낸 사람은 몇명?

좋은 알고리즘은 Precision / Recall 모두 수치가 높아야하고,

Recall 개념을 쓰면, 아까 위에서 간단하게 짠 함수는 모두 암이라고 얘기했으니, Recall = 0 인 것이 되어서 안좋은 알고리즘이다.

주의 : y=1 를 나타내는 class는 드문것에 적용해라. (여기선, 암환자)

(안그러면 위의 True Positive 4분면들이 바뀌니까… 안헷갈리기 위해서)

Trading Off Precision and Recall

Precision 과 Recall 사이에는 Trade Off가 존재한다.

암을 진단하는 예를 생각해보자.

아주 확실한 경우에만 암이라고 진단한다고 하자.(Logistic regression으로 생각해보면 h(x)>= 0.9 라고 치자)

그러면 Precision(정확도) 는 올라가고 Recall(재현율)은 내려간다.

반대로, 대충봐서 암 같으면 암이라고 진단하자. (Logistic regression으로 생각해보면 h(x)>= 0.3 라고 치자)

그러면 Recall(재현율)은 올라가고 Precision(정확도)는 내려간다.

이렇게 반비례 관계를 갖게 되는데 문제에 따라서 그래프는 오른쪽위에 보듯이 다양하게 그려진다.

그런데… Precision과 Recall이 적절하게 높도록 h(x)의 threshold를 자동으로 조절할 수 없을까?

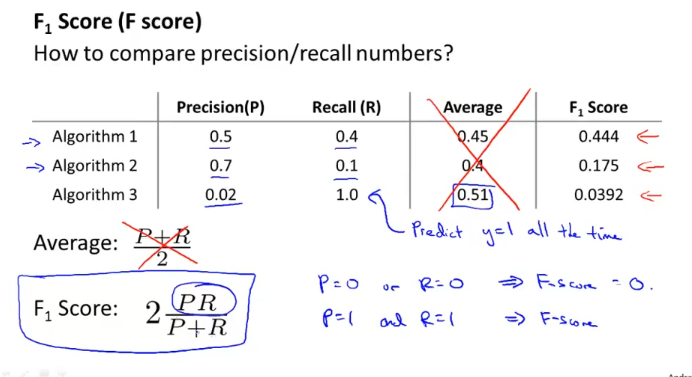
그런 개념에서 나온것이 F1 Score(also called, F Score)인데

Precision과 Recall중 하나만 높다고 좋은 알고리즘이라고 평가 할 수 없으니, 두개를 동시에 높아야 된다는 것이다.

그래서 위 알고리즘 세개를 놓고 보면 맨 마지막 세번째 알고리즘은 Recall은 높지만 Precision은 현저히 낮으므로, F Score가 안좋기때문에 좋은 알고리즘이라고 얘기할 수 없다.

Using Large Data Sets

Data For Machine Learning

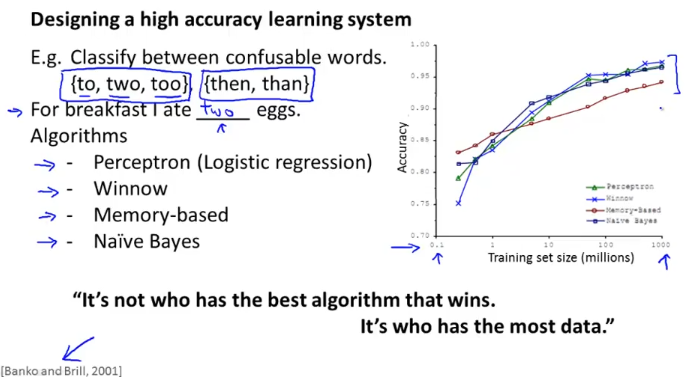
어떤 알고리즘을 쓰던 결국에 데이터가 엄청 많으면 거의 비슷한 값으로 수렴한다는 것을 볼 수가 있다..

요약하면 데이터 많이 가지고 있는게 장땡이란 소리다.