Large Margin Classification

Optimization Objective

SVM에대해 배워볼것이다.

Logistic regression의 hypothesis는 위와 같이 sigmoid 로 나타냈었다.

m = 1, 데이터가 하나인 경우에 cost function을 살펴보면 아래와 같다.

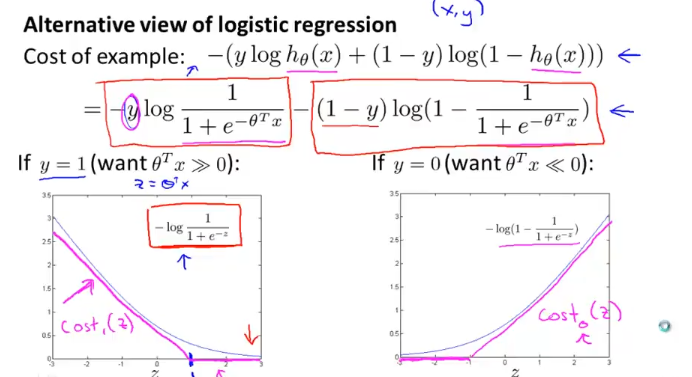
first term은 왼쪽 그래프와 같이 그려지고, second term은 오른쪽 그림인데

우리는 이 그래프의 근사치로 cost function을 정의 할것인데 위와 같이

왼쪽 cost1은 1에서 꺾이는 직선 그래프, 오른쪽 cost0은 -1에서 꺾이는 직선 그래프이다.

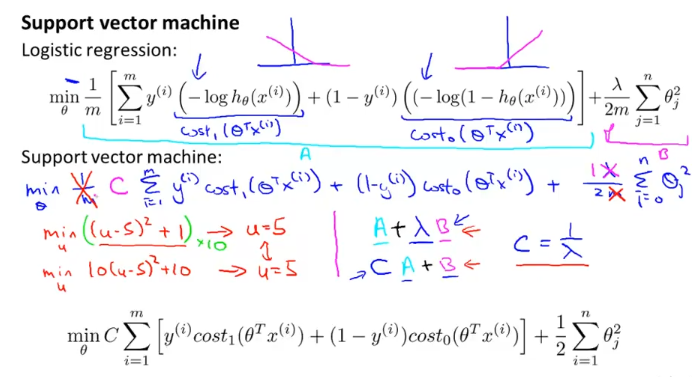
logistic regression의 항이었던 함수를 cost0, cost1으로 바꾼 결과 위와 같은 식이 나왔다.

앞으로 맨 밑에 식으로 cost function을 표현할 것인데 1/m 대신에 C를 써서 위 함수를 표현한 것 뿐이다.

Large Margin Intuition

SVM의 cost function은 위와 같은데 z(theta transpose x)의 임계값을 각각 0이 아니라 이보다 훨씬 큰 값인 1, -1로 삼았다.

위와 같이 SVM cost function에서 C가 매우 큰 값이라고 할때 파란색 네모의 값은 0에 가까워야 cost function을 minimize할 수 있다. 0으로 만들기 위한 방법은 전장의 그래프에서 봤듯이… (더이상 자세한 설명은 생략한다.)

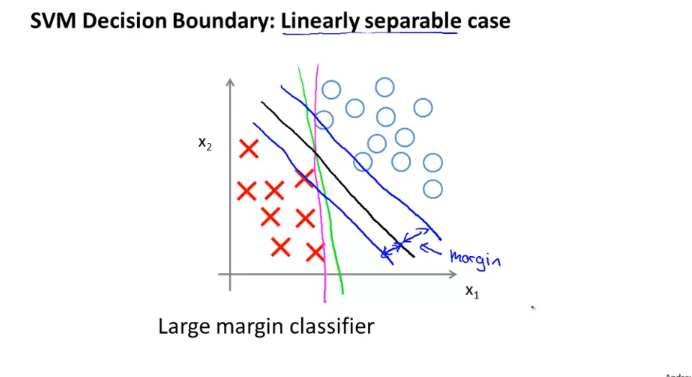
SVM을 large margin classfier라고도 하는데, 위의 그림과 같이 X,O를 구분하는 선은 여러개를 그을 수가 있는데

그중에서 X,O 사이의 “margin”이 클 수록 좋은 classifier이다. (새로운 example이 들어와도 margin이 크다면 실패 확률이 적지 않을까?)

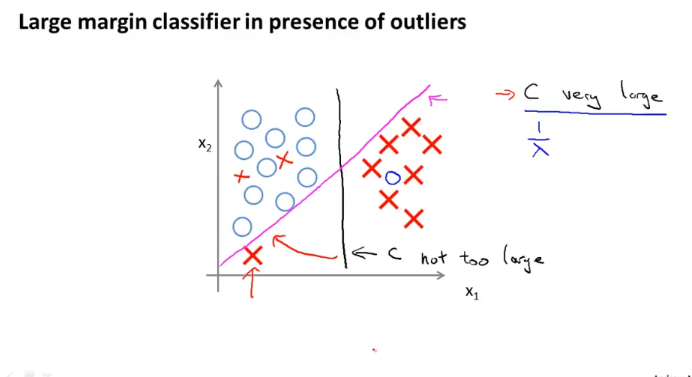
아래쪽 빨간색 X를 고려해 분홍색 라인을 그려 data를 classify하면 data에 overfitting 되는 현상이 나타난다.

C가 매우 큰 경우에 이러한 경우가 나타난다. C가 매우 크다는 것은 cost function 위 “svm_decision_boundary” 그림에서 네모친 식이 매우 작게 가야한다는 얘긴데, 이러한 경우에 overfitting 현상이 나타난다.

반면에, C가 그렇게 크지 않은 경우에는 검은색 라인처럼 그려지고, 몇몇 엇나간 데이터들은 무시한다.

The mathematics behind large margin classification (optional)

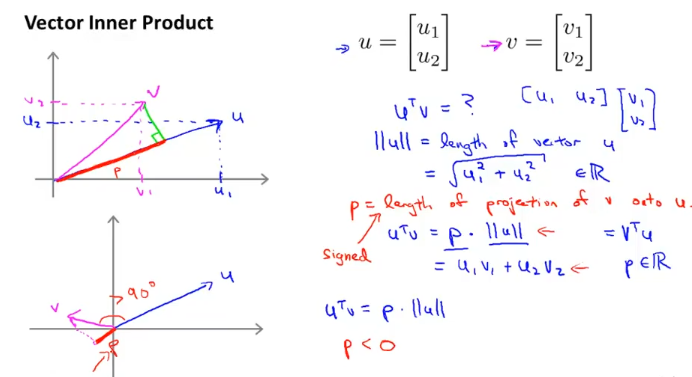
vector의 내적에 대해서 설명한 글이다. 중요하게 봐야할것은

p = length of project of v onto u

이고,

u 와 v사이의 각도가 90도가 넘을때 p < 0 인데 위와같이 선을 긋는다.

그리고 아래식이 성립한다.
$$
u^Tv = p*||u||
$$

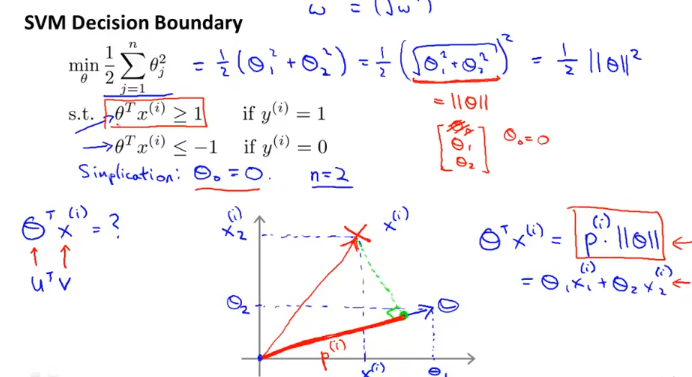
여기서는 very Large C에 대해서 얘기하려고 하여, 위의 식을 가져왔다.

비용함수의 계산은 벡터의 norm을 의미하여 1/2||theta||의 제곱 형태로 표현할 수 가있다.

n = 2 라고 했을때 이전장에서 vector의 내적에 대해 얘기한것과 같으므로
$$
\theta^Tx^{(i)} = p^{(i)}||\theta||
$$
위와 같이 표현할 수 있다.

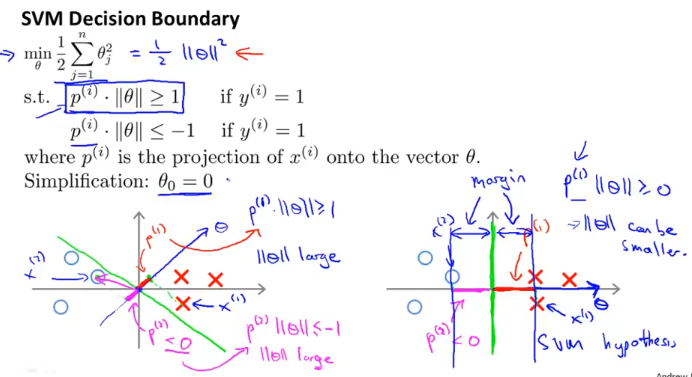
그러면 우리의 cost function의 term을 수정할수가 있는데, 위에서 적은 수식으로 표현해보면 위 그림의 파란색 박스와 같다.

새로운 식을 기준으로 왼쪽 아래의 example을 살펴보면 p_1이 매우 작은 값이 나오므로
$$
p^{(1)}||\theta|| >=1
$$
위 식이 성립하기 위해서는 ||theta|| 가 커야한다. p_2에 대해서도 마찬가지.

반면에, 오른쪽 아래 그림을 보면 classifier로 사용된 초록색 선으로 인해 p_1, p_2가 상대적으로 커지므로 ||theta||는 상대적으로 작아 질수 있다. 이로서 theta를 minimize하려고했던 우리의 목표가 달성된다.

Kernels

Kernel I

위 그래프와 같은 data에서 y =1 을 predict 하려고하면 복잡한 n차 다항식을 써야.. 할까?

저렇게 복잡한 다항식을 선택하는것은 computationally expensive하다. 그런 모델을 찾는것도 힘들다.

그래서 우리는 다른방법을 생각해본다.

l_1, l_2, l_3 점이 있다고 할때

위와같이 similarity function f1,f2,f3를 정의하고 이것을 Kernel (이것은 Gaussian Kernel)이라고 부른다.

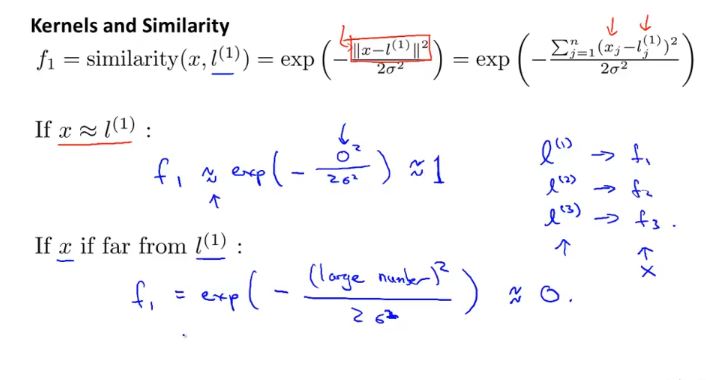
위와 같이 x가 l_1에 가까우면 우리가 정의한 similarity function은 1에 가깝게되고

x가 l_1에 멀면 우리가 정의한 similarity function은 0에 가깝게 된다.

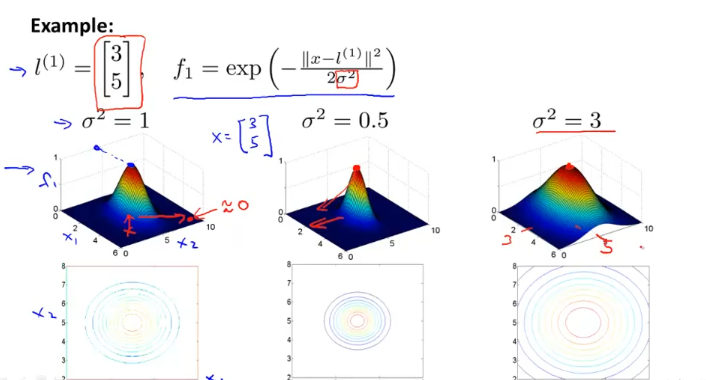
시그마 값이 작으면 작을수록 뾰족한 형태가 되고, 그래서 landmark(l_1)에서 조금만 멀어도 f값은 0에 가까워진다.

data가 하나라도 landmark에 가까우면 f 가 1이 되어 hypothesis가 1이되고, 모두다 멀면 f가 0 (그림에서 하늘색)이 된다.

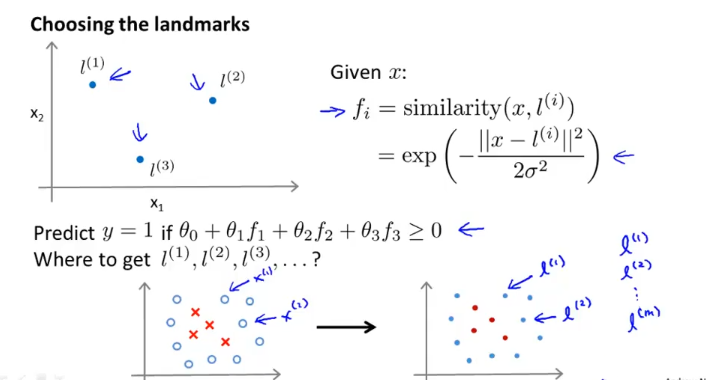
이 장에서는 landmark를 어떻게 설정할지 보여주는데 m개의 training example에 대응되도록 landmark m개를 만든다. 그리고 이 f_i를 이용해서 y를 predict한다.

이제 Kernel을 이용해 SVM의 cost function을 다시 써본다.

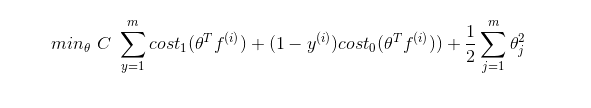
Using SVM

SVM을 구현하는 것보다 이미 구현된 라이브러리를 사용하는게 좋다.

그래도 해야하는 건

1. parameter C 결정
2. kernel 결정 (similarity function)

SVM에서 kernel을 사용하지 않을 수도있는데 이걸 linear kernel이라고 한다. (feature n이 크고, training example m이 작을때 사용한다.)

Gaussian Kernel은 feature n이 적고 training example m이 좀 더 복잡할때 주로 사용한다.

Gaussian kernel을 사용할때 feature scaling을 해줘야한다. 각 feature 간의 사이즈가 크게 다를 수 있어서 특정 feature에 치우친 결과값이 나올 수가 있기 때문이다.